题目内容
要使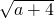 是有理数,则正整数a的最小值是________.
是有理数,则正整数a的最小值是________.
5
分析:因为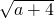 是有理数,则a+4是完全平方数,满足条件的最小正整数a为5.
是有理数,则a+4是完全平方数,满足条件的最小正整数a为5.
解答:∵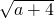 是有理数,
是有理数,
∴a+4是完全平方数;
又∵a是正整数,
∴a+4≥9,即a≥5;
∴正整数a的最小值是5.
故答案是:5.
点评:主要考查了乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数.二次根式的运算法则:乘法法则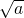
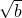 =
=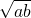 .除法法则
.除法法则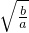 =
= .解题关键是分解成一个完全平方数和一个代数式的积的形式.
.解题关键是分解成一个完全平方数和一个代数式的积的形式.
分析:因为
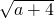 是有理数,则a+4是完全平方数,满足条件的最小正整数a为5.
是有理数,则a+4是完全平方数,满足条件的最小正整数a为5.解答:∵
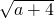 是有理数,
是有理数,∴a+4是完全平方数;
又∵a是正整数,
∴a+4≥9,即a≥5;
∴正整数a的最小值是5.
故答案是:5.
点评:主要考查了乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数.二次根式的运算法则:乘法法则
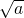
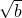 =
=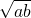 .除法法则
.除法法则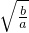 =
= .解题关键是分解成一个完全平方数和一个代数式的积的形式.
.解题关键是分解成一个完全平方数和一个代数式的积的形式. 
练习册系列答案
相关题目