题目内容
 如图,△ABC中任意一点P(x0,y0),将△ABC平移后,点P的对应点为P1(x0+6,y0+4).
如图,△ABC中任意一点P(x0,y0),将△ABC平移后,点P的对应点为P1(x0+6,y0+4).(1)写出△ABC中A、B、C分别对应的点A1、B1、C1的坐标,并画出△A1B1C1.
(2)若△ABC外有一点M经过同样的平移后得到点N(5,3),写出M点关于原点对称的点M′的坐标.
分析:(1)先根据点P(x0,y0)平移后得到P1(x0+6,y0+4)的平移规律,根据此规律得出点A1、B1、C1的坐标,并画出△A1B1C1;
(2)由(1)中的平移规律求出点M的坐标,再根据关于原点对称的点的坐标特点求出点M′的坐标即可.
(2)由(1)中的平移规律求出点M的坐标,再根据关于原点对称的点的坐标特点求出点M′的坐标即可.
解答: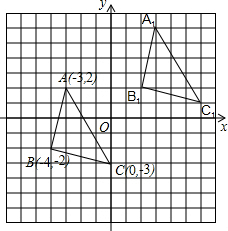 解:(1)∵,△ABC中任意一点P(x0,y0),将△ABC平移后,点P的对应点为P1(x0+6,y0+4).
解:(1)∵,△ABC中任意一点P(x0,y0),将△ABC平移后,点P的对应点为P1(x0+6,y0+4).
∴△ABC应先向右移动6格,再向上移动4格,
∵A(-3,2),B(-4,-2),C(0,-3),
∴平移后A1(3,6),B1(2,2),C1(6,1),
如图所示:
(2)∵M经过同样的平移后得到点N(5,3),
∴M(5-6,3-4),即M(-1,-1),
∴M′(1,1).
 解:(1)∵,△ABC中任意一点P(x0,y0),将△ABC平移后,点P的对应点为P1(x0+6,y0+4).
解:(1)∵,△ABC中任意一点P(x0,y0),将△ABC平移后,点P的对应点为P1(x0+6,y0+4).∴△ABC应先向右移动6格,再向上移动4格,
∵A(-3,2),B(-4,-2),C(0,-3),
∴平移后A1(3,6),B1(2,2),C1(6,1),
如图所示:
(2)∵M经过同样的平移后得到点N(5,3),
∴M(5-6,3-4),即M(-1,-1),
∴M′(1,1).
点评:本题考查的是作图-平移变换,熟知平面直角坐标系内:上加下减、左加右减的规律是解答此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
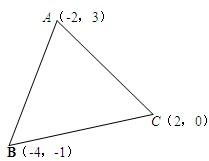 19、如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1.画出△A1B1C1,并求A1,B1,C1的坐标.
19、如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1.画出△A1B1C1,并求A1,B1,C1的坐标.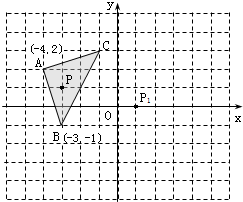 22、如图,△ABC中任意一点P(x0,y0)经过平移后对应点为P1(x0+4,y0-1).
22、如图,△ABC中任意一点P(x0,y0)经过平移后对应点为P1(x0+4,y0-1).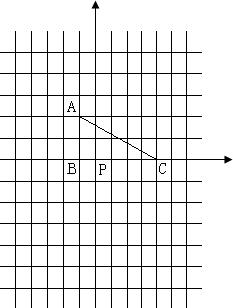 22、如图,△ABC中任意一点P(xo,yo),将△ABC平移后,点P的对应点P1(xo+6,yo+4).
22、如图,△ABC中任意一点P(xo,yo),将△ABC平移后,点P的对应点P1(xo+6,yo+4).