ΧβΡΩΡΎ»ί
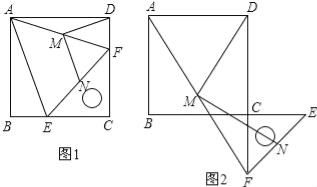
ΓΨΧβΡΩΓΩ‘ΎΥΡ±Ώ–ΈABDC÷–Θ§ACΘΫABΘ§DCΘΫDBΘ§ΓœCABΘΫ60ΓψΘ§ΓœCDBΘΫ120ΓψΘ§E «AC…œ“ΜΒψΘ§F «AB―”≥ΛœΏ…œ“ΜΒψΘ§«“CEΘΫBFΘ°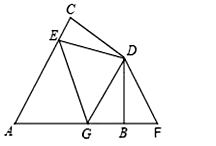
Θ®1Θ© ‘ΥΒΟςΘΚDEΘΫDFΘΜ
Θ®2Θ©‘ΎΆΦ÷–Θ§»τG‘ΎAB…œ«“ΓœEDGΘΫ60ΓψΘ§ ‘≤¬œκCEΓΔEGΓΔBG÷°ΦδΒΡ ΐΝΩΙΊœΒ≤Δ÷ΛΟς¥ΥΫα¬έΘΜ
Θ®3Θ©»τΧβ÷–ΧθΦΰΓΑΓœCABΘΫ60ΓψΘ§ΓœCDBΘΫ120ΓψΓ±ΗΡΈΣΓœCABΘΫΠΝΘ§ΓœCDBΘΫ180ΓψΘ≠ΠΝΘ§G‘ΎAB…œΘ§ΓœEDG¬ζΉψ ≤Ο¥ΧθΦΰ ±Θ§(2)÷–Ϋα¬έ»‘»Μ≥…ΝΔΘΩΘ®÷Μ–¥ΫαΙϊ≤Μ“Σ÷ΛΟςΘ©Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚΓΏΓœCAB+ΓœC+ΓœCDB+ΓœABD=360ΓψΘ§ΓœCAB=60ΓψΘ§ΓœCDB=120ΓψΘ§
ΓύΓœC+ΓœABD=360Γψ©¹60Γψ©¹120Γψ=180ΓψΘ§
”÷ΓΏΓœDBF+ΓœABD=180ΓψΘ§
ΓύΓœC=ΓœDBFΘ§
‘ΎΓςCDEΚΆΓςBDF÷–Θ§
ΓύΓςCDEΓ’ΓςBDFΘ®SASΘ©Θ§
ΓύDE=DF.
Θ®2Θ©
ΫβΘΚ»γΆΦ1Θ§Ν§Ϋ”ADΘ§≤¬œκCEΓΔEGΓΔBG÷°ΦδΒΡ ΐΝΩΙΊœΒΈΣΘΚCE+BG=EGΘ°
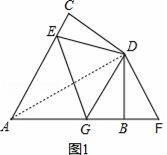
÷ΛΟςΘΚ‘ΎΓςABDΚΆΓςACD÷–Θ§
![]()
ΓύΓςABDΓ’ΓςACDΘ®SSSΘ©Θ§
ΓύΓœBDA=ΓœCDA= ![]() ΓœCDB=
ΓœCDB= ![]() ΓΝ120Γψ=60ΓψΘ§
ΓΝ120Γψ=60ΓψΘ§
”÷ΓΏΓœEDG=60ΓψΘ§
ΓύΓœCDE=ΓœADGΘ§ΓœADE=ΓœBDGΘ§
”…Θ®1Θ©Ω…÷ΣΓςCDEΓ’ΓςBDFΘ§
ΓύΓœCDE=ΓœBDFΘ§
ΓύΓœBDG+ΓœBDF=60ΓψΘ§
Φ¥ΓœFDG=60ΓψΘ§
ΓύΓœEDG=ΓœFDGΘ§
‘ΎΓςDEGΚΆΓςDFG÷–Θ§
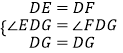
ΓύΓςDEGΓ’ΓςDFGΘ§
ΓύEG=FGΘ§
”÷ΓΏCE=BFΘ§FG=BF+BGΘ§
ΓύCE+BG=EG
Θ®3Θ©
ΫβΘΚ“Σ ΙCE+BG=EG»‘»Μ≥…ΝΔΘ§
‘ρΓœEDG=ΓœBDA=ΓœCDA= ![]() ΓœCDBΘ§
ΓœCDBΘ§
Φ¥ΓœEDG= ![]() Θ®180Γψ©¹ΠΝΘ©=90Γψ©¹
Θ®180Γψ©¹ΠΝΘ©=90Γψ©¹ ![]() ΠΝΘ§
ΠΝΘ§
ΓύΒ±ΓœEDG=90Γψ©¹ ![]() ΠΝ ±Θ§ CE+BG=EG»‘»Μ≥…ΝΔ
ΠΝ ±Θ§ CE+BG=EG»‘»Μ≥…ΝΔ
ΓΨΫβΈωΓΩΘ®1Θ© Ήœ»≈–Εœ≥ωΓœC=ΓœDBFΘ§»ΜΚσΗυΨί»ΪΒ»»ΐΫ«–Έ≈–Ε®ΒΡΖΫΖ®Θ§≈–Εœ≥ωΓςCDEΓ’ΓςBDFΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…≈–Εœ≥ωDE=DFΘ°
Θ®2Θ©≤¬œκCEΓΔEGΓΔBG÷°ΦδΒΡ ΐΝΩΙΊœΒΈΣΘΚCE+BG=EGΘ° Ήœ»ΗυΨί»ΪΒ»»ΐΫ«–Έ≈–Ε®ΒΡΖΫΖ®Θ§≈–Εœ≥ωΓςABDΓ’ΓςACDΘ§Φ¥Ω…≈–Εœ≥ωΓœBDA=ΓœCDA=60ΓψΘΜ»ΜΚσΗυΨίΓœEDG=60ΓψΘ§Ω…ΒΟΓœCDE=ΓœADGΘ§ΓœADE=ΓœBDGΘ§‘ΌΗυΨίΓœCDE=ΓœBDFΘ§≈–Εœ≥ωΓœEDG=ΓœFDGΘ§Ψί¥ΥΆΤΒΟΓςDEGΓ’ΓςDFGΘ§Υυ“‘EG=FGΘ§ΉνΚσΗυΨίCE=BFΘ§≈–Εœ≥ωCE+BG=EGΦ¥Ω…Θ°
Θ®3Θ©ΗυΨίΘ®2Θ©ΒΡ÷ΛΟςΙΐ≥ΧΘ§“Σ ΙCE+BG=EG»‘»Μ≥…ΝΔΘ§‘ρΓœEDG=ΓœBDA=ΓœCDA= ![]() ΓœCDBΘ§Φ¥ΓœEDG=
ΓœCDBΘ§Φ¥ΓœEDG= ![]() Θ®180Γψ-ΠΝΘ©=90Γψ-
Θ®180Γψ-ΠΝΘ©=90Γψ- ![]() ΠΝΘ§Ψί¥ΥΫβ¥πΦ¥Ω…Θ°
ΠΝΘ§Ψί¥ΥΫβ¥πΦ¥Ω…Θ°

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ