题目内容
【题目】已知平面直角坐标系中两定点A（﹣1，0）、B（4，0），抛物线y=ax2+bx﹣2（a≠0）过点A，B，顶点为C，点P（m，n）（n＜0）为抛物线上一点．
（1）求抛物线的解析式和顶点C的坐标；
（2）当∠APB为钝角时，求m的取值范围；
（3）若m＞
，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜
）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得首位依次连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．
【答案】(1) 抛物线的解析式为：y=
x2﹣
x﹣2；C（ ，﹣
）．(2) ﹣1＜m＜0或3＜m＜4;(3)
【解析】分析：（1）待定系数法求解析式即可，求得解析式后转换成顶点式即可．
（2）因为AB为直径，所以当抛物线上的点P在⊙C的内部时，满足∠APB为钝角，所以-1＜m＜0，或3＜m＜4．
（3）左右平移时，使A′D+DB″最短即可，那么作出点C′关于x轴对称点的坐标为C″，得到直线P″C″的解析式，然后把A点的坐标代入即可．
详解：（1）∵抛物线y=ax2+bx﹣2（a≠0）过点A，B，
∴
，
解得：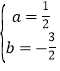
，
∴抛物线的解析式为：y=x2﹣x﹣2；
∵y=x2﹣x﹣2=（x﹣）2﹣，
∴C（，﹣）．
（2）如图1，以AB为直径作圆M，则抛物线在圆内的部分，能使∠APB为钝角，
∴M（，0），⊙M的半径=
．
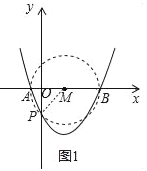
∵P′是抛物线与y轴的交点，
∴OP′=2，
∴MP′=
，
∴P′在⊙M上，
∴P′的对称点（3，﹣2），
∴当﹣1＜m＜0或3＜m＜4时，∠APB为钝角．
（3）存在；
抛物线向左或向右平移，因为AB、P′C′是定值，所以A、B、P′、C′所构成的多边形的周长最短，只要AC′+BP′最小；
第一种情况：抛物线向右平移，AC′+BP′＞AC+BP，
第二种情况：向左平移，如图2所示，由（2）可知P（3，﹣2），
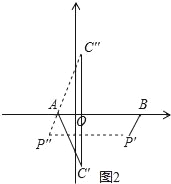
又∵C（，﹣）
∴C'（﹣t，﹣），P'（3﹣t，﹣2），
∵AB=5，
∴P″（﹣2﹣t，﹣2），
要使AC′+BP′最短，只要AC′+AP″最短即可，
点C′关于x轴的对称点C″（﹣t，），
设直线P″C″的解析式为：y=kx+b，
，
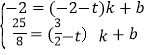解得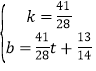
∴直线y=
，
当P″、A、C″在一条直线上时，周长最小，
∴
=0
∴t=．
故将抛物线向左平移个单位连接A、B、P′、C′所构成的多边形的周长最短．
