Question

已知关于x的一元二次方程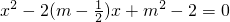有两个不相等的实数根x₁，x₂，且满足x₁²+x₂²-x₁x₂=12，则m的值为

1. A.
   m=-1
2. B.
   m=5
3. C.
   m=-1或m=5
4. D.
   m=1或m=-5

Answer 1

A
分析：由方程有两个不等的实数根，得到根的判别式大于0，列出关于m的不等式，求出不等式的解集得到m的范围，利用根与系数的关系求出两根之和与两根之积，把已知的等式配方得到关于两根之和与两根之积的形式，将得出的两根之和与两根之积代入列出关于m的方程，求出方程的解即可得到m的值．
解答：∵方程有两个不相等的实数根，
∴△=b²-4ac=4（m-）²-4（m²-2）＞0，
即4m＜9，解得m＜，
根据根与系数的关系得：x₁+x₂=2（m-），x₁x₂=m²-2，
∴x₁²+x₂²-x₁x₂=（x₁+x₂）²-3x₁x₂=4（m-）²-3（m²-2）=12，
整理得：（m-5）（m+1）=0，
解得：m₁=5（舍去），m₂=-1，
则m的值为-1．
故选A
点评：此题考查了一元二次方程根与系数的关系，完全平方公式以及根的判别式的运用，若一元二次方程有解，即△=b²-4ac≥0时，设方程的两个根分别为x₁，x₂，则有x₁+x₂=-，x₁x₂=，熟练掌握此关系是解本题的关键，同时注意求出m后要根据m的范围对m进行合理的取舍．