题目内容
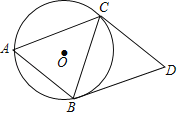
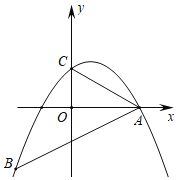
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
x2+bx+c的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)求此二次函数的解析式;
(2)证明:AO平分∠BAC;
(3)在二次函数对称轴上是否存在一点P使得AP=BP?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)见解析;(3)存在.点P的坐标为(1,﹣4);
x+2;(2)见解析;(3)存在.点P的坐标为(1,﹣4);
【解析】
(1)将点A(4,0)与点B(4,4)代入函数解析式即可;
(2)求出直线AB的解析式,求出AB与y轴交点D(0,2),可得OC=OD,再由AO⊥CD,可证AO平分∠BAC;
(3)二次函数的对称轴为直线x=1,设点P的坐标为(1,m),AP2=(41)2+m2,BP2=(1+4)2+(m4)2,当AP=BP时,求出m=4即可;
(1)∵点A(4,0)与点B(﹣4,4)在二次函数的图象上,
∴![]() ,
,
解得![]() ,
,
∴二次函数的解析式为y=![]() ;
;
(2)设直线AB的解析式为y=ax+n
则有![]() ,
,
解得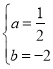 ,
,
故直线AB的解析式为y=![]() x﹣2,
x﹣2,
设直线AB与y轴的交点为点D,
x=0,
则y=﹣2,
故点D为(0,﹣2),
由(1)可知点C为(0,2),
∴OC=OD
又∵AO⊥CD,
∴AO平分∠BAC;
(3)存在.
∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() +2,
+2,
∴二次函数的对称轴为直线x=1,
设点P的坐标为(1,m),
AP2=(4﹣1)2+m2,BP2=(1+4)2+(m4)2,
当AP=BP时,AP2=BP2,
则有9+m2=25+m2+16+8m,
解得m=﹣4,
∴点P的坐标为(1,﹣4);

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目