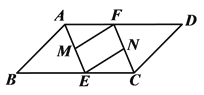题目内容
【题目】如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.

(1) 求线段AD的长.
(2) 在线段BC上是否存在点P,使△APD是等腰三角形,若存在,求出线段BP的长;若不存在,请说明理由.
【答案】(1)AD =5;(2)在线段BC上是否存在点P,使△APD是等腰三角形,此时线段BP的长为3或![]() .
.
【解析】试题分析:(1)过点D作DE⊥AB于E点,由可判断四边形BCDE要矩形,然后通过勾股定理即可求得AD的长;
(2)分AP=AD、PA=PD这两种情况进行讨论即可得.
试题解析:(1)过D作DE⊥AB于E点,
由AB⊥BC,DC⊥BC ,则可得四边形BCDE是矩形,∴BE=DC=1,DE=BC=4,∵AB=4,∴AE=AB-BE=1,∵∠AED=90°,∴AD=![]() =5;
=5;

(2)如图1,当AP=AD=5时,∵∠B=90°,∴BP=![]() =3;
=3;
如图2,当PA=PD时,∵∠B=∠C=90°,∴AB2+BP2=DC2+PC2,即42+BP2=12+(4-BP)2,∴BP=![]() ;
;
综上,在线段BC上是否存在点P,使△APD是等腰三角形,此时线段BP的长为3或![]() .
.



【题目】某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目 | 第一次锻炼 | 第二次锻炼 | ||
步数(步) | 10000 | ① | ||
平均步长(米/步) | 0.6 | ② | ||
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.