题目内容
【题目】如图,在□ABCD中,∠BAD和∠DCB的平分线AE、CF分别交BC、AD于点E、F,点M、N分别为AE、CF的中点,连接FM、EN.试判断FM和EN的数量关系和位置关系,并加以证明.
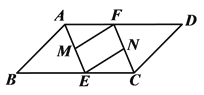
【答案】FM=EN,FM//EN.证明见解析.
【解析】试题分析:先根据已知证四边形AECF是平行四边形,再证明四边形ENFM是平行四边形即可得.
试题解析:FM=EN,FM//EN.证明如下:
∵四边形ABCD是平行四边形,∴∠BAD=∠DCB,AD∥BC,
∵AE、CF分别平分∠BAD和∠DCB,∴∠BAE=∠DAE=![]() ∠BAD,
∠BAD,
∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴BA=BE,
同理可证DF=DC,
∵AB=CD,AD=BC,∴DF=BE,∴AF=EC,
∵AF∥EC,∴四边形AECF是平行四边形.∴AE![]() CF,
CF,
∵EM=![]() AE,FN=
AE,FN=![]() CF,∴EM
CF,∴EM![]() FN,∴四边形ENFM是平行四边形,
FN,∴四边形ENFM是平行四边形,
∴FM=EN,FM//EN.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

