题目内容
如图,已知A(0,1)、D(4,3),P是以AD为对角线的矩形ABDC内部(不在各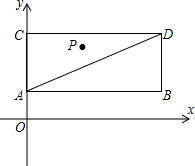 边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.
边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.
(1)能否判断抛物线y=ax2+bx+1的开口方向?请说明理由.
(2)设抛物线y=ax2+bx+1与x轴有交点F、E(F在E的左侧),△EAO与△FAO的面积之差为3,且这条抛物线与线段AD有一个交点的横坐标为 ,这时能确定a、b的值吗?若能,请求出a、b的值;若不能,请确定a、b的取值范围.(本题的图形仅供分析参考用)
,这时能确定a、b的值吗?若能,请求出a、b的值;若不能,请确定a、b的取值范围.(本题的图形仅供分析参考用)
解:(1)能判断抛物线开口向下.
∵y=ax2+bx+1经过点A(0,1),
∴点P的位置高于点A,说明点P不是抛物线的最低点,
∴点P是抛物线的最高点.
∴抛物线y=ax2+bx+1的开口向下.
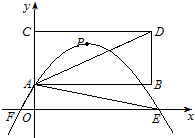 (2)如图,设抛物线与x轴的交点坐标为F(x1,0)、E(x2,0),
(2)如图,设抛物线与x轴的交点坐标为F(x1,0)、E(x2,0),
则x1<0,x2>0
S△AEO= OE•OA=
OE•OA= x2;
x2;
S△AFO= OF•OA=
OF•OA= x1
x1
∵S△AEO-S△AFO=3
∴ x2-(
x2-( x1)=3,即x1+x2=6
x1)=3,即x1+x2=6
∵x1+x2= +
+ =
=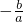
∴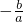 =6,即b=-6a①
=6,即b=-6a①
另一方面,设直线AD的解析式为y=kx+m,
并把点A(0,1)、D(4,3)的坐标代入解析式得 ,解得
,解得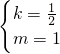 ,∴
,∴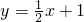
由于抛物线与线段AD有一个交点的横坐标为 ,所以纵坐标=
,所以纵坐标=
把点( ,
,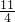 )的坐标代入y=ax2+bx+1,
)的坐标代入y=ax2+bx+1,
整理得49a+14b=7②
解由①②组成的方程组得 ,
,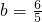 .
.
分析:(1)由y=ax2+bx+1可知抛物线过点(0,1),即A点,而顶点P在正方形内部,可判断抛物线开口向下;
(2)已知OA=1,设F(x1,0)、E(x2,0),利用△EAO与△FAO的面积之差为3,可求x1+x2=6的值,再利用两根关系求a、b的一个关系式,求直线AD的解析式,根据D点横坐标为 ,求D点纵坐标,代入抛物线解析式,得到a、b的另外一个关系式,解方程组求a、b的值.
,求D点纵坐标,代入抛物线解析式,得到a、b的另外一个关系式,解方程组求a、b的值.
点评:本题考查了二次函数的综合运用.关键是根据抛物线的顶点不是最高点,就是最低点,判断开口方向,根据面积关系,及抛物线所经过的点,列方程组求a、b的值.
∵y=ax2+bx+1经过点A(0,1),
∴点P的位置高于点A,说明点P不是抛物线的最低点,
∴点P是抛物线的最高点.
∴抛物线y=ax2+bx+1的开口向下.
 (2)如图,设抛物线与x轴的交点坐标为F(x1,0)、E(x2,0),
(2)如图,设抛物线与x轴的交点坐标为F(x1,0)、E(x2,0),则x1<0,x2>0
S△AEO=
 OE•OA=
OE•OA= x2;
x2;S△AFO=
 OF•OA=
OF•OA= x1
x1∵S△AEO-S△AFO=3
∴
 x2-(
x2-( x1)=3,即x1+x2=6
x1)=3,即x1+x2=6∵x1+x2=
 +
+ =
=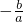
∴
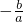 =6,即b=-6a①
=6,即b=-6a①另一方面,设直线AD的解析式为y=kx+m,
并把点A(0,1)、D(4,3)的坐标代入解析式得
 ,解得
,解得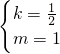 ,∴
,∴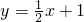
由于抛物线与线段AD有一个交点的横坐标为
 ,所以纵坐标=
,所以纵坐标=
把点(
 ,
,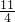 )的坐标代入y=ax2+bx+1,
)的坐标代入y=ax2+bx+1,整理得49a+14b=7②
解由①②组成的方程组得
 ,
,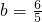 .
.分析:(1)由y=ax2+bx+1可知抛物线过点(0,1),即A点,而顶点P在正方形内部,可判断抛物线开口向下;
(2)已知OA=1,设F(x1,0)、E(x2,0),利用△EAO与△FAO的面积之差为3,可求x1+x2=6的值,再利用两根关系求a、b的一个关系式,求直线AD的解析式,根据D点横坐标为
 ,求D点纵坐标,代入抛物线解析式,得到a、b的另外一个关系式,解方程组求a、b的值.
,求D点纵坐标,代入抛物线解析式,得到a、b的另外一个关系式,解方程组求a、b的值.点评:本题考查了二次函数的综合运用.关键是根据抛物线的顶点不是最高点,就是最低点,判断开口方向,根据面积关系,及抛物线所经过的点,列方程组求a、b的值.

练习册系列答案
相关题目
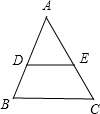 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
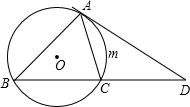 =2,∠ADC=30°
=2,∠ADC=30°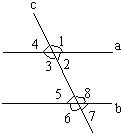 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
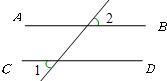 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=