题目内容
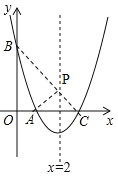
【题目】如图,抛物线![]() 交x轴于点
交x轴于点![]() ,交y轴于点B,对称轴是直线
,交y轴于点B,对称轴是直线![]() .
.
(1)求抛物线的解析式;
(2)P是抛物线对称轴上的一个动点,是否存在点P,使![]() 的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
()根据对称轴和点A坐标列方程组求出b、c的值即可得答案;(2)设C点为抛物线与x轴的另一个交点,连接![]() ,与
,与![]() 交于点P,根据二次函数的对称性可得PA=PC,点C坐标,根据两点之间,线段最短可得P点即为所求,利用待定系数法求出直线BC的解析式,把x=2代入即可求出P点坐标.
交于点P,根据二次函数的对称性可得PA=PC,点C坐标,根据两点之间,线段最短可得P点即为所求,利用待定系数法求出直线BC的解析式,把x=2代入即可求出P点坐标.
(1)由题意得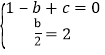 ,
,
解得![]() .
.
∴抛物线解析式为![]() .
.
(2)设C点为抛物线与x轴的另一个交点,连接![]() ,与
,与![]() 交于点P,
交于点P,
∵点A与点C关于x=2对称,A(1,0)
∴PA=PC,C(3,0)
∵两点之间,线段最短,
∴PA+PB+AB=BC+AB,即△PAB的周长为最小值.
∵x=0时,y=3,
∴B(0,3),
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .
.
当x=2时,y=-2+3=1
∴![]() .
.
即存在点P,使![]() 的周长最小,点P坐标为(2,1).
的周长最小,点P坐标为(2,1).

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】春华中学为了解九年级学生的身高情况,随机抽测50名学生的身高后,所得部分资料如下(身高单位:![]() ,测量时精确到
,测量时精确到![]() ):
):
身高 | 148 | 151 | 154 | 155 | 157 | 158 | 160 | 161 | 162 | 164 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 3 | 4 | 5 |
身高 | 165 | 166 | 167 | 168 | 170 | 171 | 173 | 175 | 177 | 179 |
人数 | 2 | 3 | 6 | 1 | 4 | 2 | 3 | 1 | 1 | 1 |
若将数据分成8组,取组距为![]() ,相应的频率分布表(部分)是:
,相应的频率分布表(部分)是:
分组 | 频数 | 频率 |
147.5~151.5 | 2 | 0.04 |
151.5~155.5 | 3 | 0.06 |
155.5~159.5 | 5 | 0.10 |
159.5~163.5 | 11 | 0.22 |
163.5~167.5 | ________ | ________ |
167.5~171.5 | 7 | 0.14 |
171.5~175.5 | 4 | 0.08 |
175.5~179.5 | 2 | 0.04 |
合计 | 50 | 1.00 |
请回答下列问题:
(1)样本数据中,学生身高的众数、中位数各是多少?
(2)填写频率分布表中未完成的部分;
(3)若该校九年级共有850名学生,请你估计该年级学生身高在![]() 及以上的人数.
及以上的人数.