题目内容
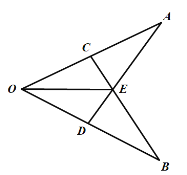
【题目】如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有___________对.
【答案】4.
【解析】
由于OA=OB,∠AOD=∠BOC,OC=OD,利用SAS可证△AOD≌△BOC,再利用全等三角形的性质,可知∠A=∠B;在△ACE和△BDE中,∠A=∠B,∠AEC=∠BED,而OA-OC=OB-OD,即AC=BD,利用AAS可证△ACE≌△BDE;再利用全等三角形的性质,可得AE=BE,在△AOE和△BOE中,由于OA=OB,∠A=∠B,AE=BE,利用SAS可证△AOE≌△BOE;再利用全等三角形的性质,可得∠COE=∠DOE,而OE=OE,OC=OD,利用SAS可证△COE≌△DOE.
解:∵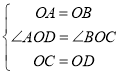 ,
,
∴△AOD≌△BOC(SAS),
∴∠A=∠B,
又∵∠AEC=∠BED,OA-OC=OB-OD,
即AC=BD,
∴△ACE≌△BDE,
∴AE=BE,
又∵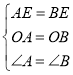
∴△AOE≌△BOE(SAS),
∴∠COE=∠DOE,
又∵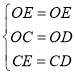 ,
,
∴△COE≌△DOE(SSS).
故全等的三角形一共有4对.
故答案为4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目