Question

函数y=-x+4的图象分别交x轴，y轴于点N、M，过线段MN上的点A向x轴作垂线与x轴交于A₁（a，0），绕着O点顺时针旋转射线OA，交MN于另一点B，过B点也向x轴作垂线与x轴交于B₁（b，0），且b＞a．
（1）△OA₁A与△OB₁B的面积分别用S₁、S₂表示，当a+b满足什么条件时，S₂＞S₁．
（2）当a=2，b=3时，若一抛物线经过N、A、O三点，且对称轴与OB交于点D，点P为线段DB上一点，过P点作y轴的平行线，交抛物线于点G．问：是否存在这样的点P，使得四边形ADPG为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

Answer 1

分析：（1）把点A₁、B₁的横坐标代入直线求出点A、B的坐标，然后根据三角形的面积表示出S₁、S₂，再根据S₂＞S₁列出关于a、b的不等式，整理后求解即可；
（2）根据直线解析式求出点N的坐标，然后利用待定系数法求出二次函数的解析式，然后判断出点A是二次函数的顶点，再根据AD、PG平行于y轴可得AD、PG是底边，AG、DP是等腰梯形的腰，再根据b的值求出点B的坐标，然后求出直线OB的解析式，根据抛物线的解析式与OB的解析式求出AD的长，设点P的横坐标为m，表示出PG的长度，过点P作PE⊥AD于E，表示出PE，PE∥x轴，根据两直线平行，内错角相等求出∠EPD=∠BOB₁，判断出△DPE和△BOB₁相似，根据相似三角形对应边成比例列式求出DE，再根据等腰梯形的性质，PG=AD-2DE，然后列出方程求出m的值，即可得到点P的坐标．

解答：解：（1）把A₁（a，0），B₁（b，0）的横坐标代入直线y=-x+4得，
y=-a+4，y=-b+4，
所以，A（a，-a+4），B（b，-b+4），
所以，S₁=

1

2

a•（-a+4）=-

1

2

a²+2a，
S₂=

1

2

b•（-b+4）=-

1

2

b²+2b，
∵S₂＞S₁，
∴-

1

2

b²+2b＞-

1

2

a²+2a，
整理得，a²-b²+4b-4a＞0，
即（a-b）（a+b-4）＞0，
∵a＜b，
∴a-b＜0，
∴a+b-4＜0，
∴a+b＜4，
即当a+b＜4时，S₂＞S₁；

（2）当a=2时，y=-2+4=2，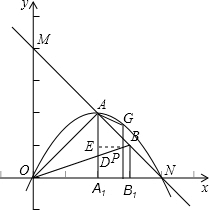
∴点A的坐标为（2，2），
y=0时，-x+4=0，
解得x=4，
∴点N（4，0），
设经过N（4，0）、A（2，2）、O（0，0）的抛物线为y=ax²+bx，
则

16a+4b=0 4a+2b=2

，
解得

a=- 1 2 b=2

，
所以，抛物线解析式为y=-

1

2

x²+2x=-

1

2

（x-2）²+2，
所以，点A（2，2）是抛物线的顶点，
所以，直线AA₁就是抛物线的对称轴，AD、PG是底边，AG、DP是等腰梯形的腰，
b=3时，y=-3+4=1，
∴点B的坐标为（3，1），
易求直线OB的解析式为y=

1

3

x，
x=2时，y=

2

3

，
∴点D的坐标为（2，

2

3

），
∴AD=2-

2

3

=

4

3

，
设点P的横坐标为m，则点P的坐标为（m，

1

3

m），点G的坐标为（m，-

1

2

m²+2m），
∴PG=-

1

2

m²+2m-

1

3

m=-

1

2

m²+

5

3

m，
过点P作PE⊥AD于E，则PE=m-2，PE∥x轴，
∴∠EPD=∠BOB₁，
∴△DPE∽△BOB₁，
∴

PE

OB1

=

DE

BB1

，
即

m-2

3

=

DE

1

，
解得DE=

m-2

3

，
∵四边形ADPG为等腰梯形，
∴PG=AD-2DE，
即-

1

2

m²+

5

3

m=

4

3

-2×

m-2

3

，
整理得，3m²-14m+16=0，
解得m₁=

8

3

，m₂=2（P、D重合，不符合题意，舍去），

1

3

m=

1

3

×

8

3

=

8

9

，
所以，点P的坐标为（

8

3

，

8

9

），
故，存在点P（

8

3

，

8

9

），使得四边形ADPG为等腰梯形．

点评：本题是二次函数综合题型，主要考查了一次函数图象上点的坐标特征，待定系数法求二次函数解析式，三角形的面积，等腰梯形的性质，（2）难度较大，根据二次函数解析式与直线解析式表示出AD、PG的长，再根据等腰梯形的性质列出方程是解题的关键，也是本题的难点，作出图形更形象直观．