题目内容
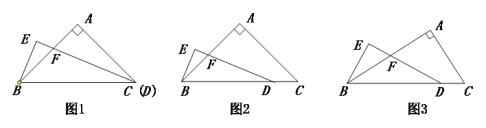
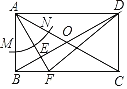
【题目】如图,在矩形ABCD中,对角线AC与BD交于点O,已知AB=OA,按以下步骤作图:①以点A为圆心,以任意长为半径画弧交AB于M,交AC于点N;②分别以点M,N为圆心,以大于![]() MN为半径画弧,两弧相交于点E;③作射线AE交BC于点F,连接DF.若AB=
MN为半径画弧,两弧相交于点E;③作射线AE交BC于点F,连接DF.若AB=![]() ,则线段DF的长为_____.
,则线段DF的长为_____.
【答案】![]()
【解析】
根据四边形ABCD是矩形,和AB=OA,可得△ABO是等边三角形,由作图过程可得,AF是∠BAO的平分线,再根据勾股定理即可求出DF的长.
解:∵四边形ABCD是矩形,
∴AO=CO=OB=OD,
∵AB=OA,
∴AB=OA=OB=![]() ,
,
∴△ABO是等边三角形,
∴∠BAO=60°,
∵AC=2AO=2![]() ,
,
∴AD=BC=![]() =3,
=3,
由作图过程可知:
AF是∠BAO的平分线,
∴∠BAF=∠FAC=30°,
∴BF=ABtan30°=1,
∴CF=BC﹣BF=3﹣1=2,
∴DF=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目