题目内容
七年级我们学过三角形的相关知识,在动手实践的过程中,发现了一个基本事实:三角形的三条高(或三条高所在直线)相交于一点.其实,有很多八年级、九年级的问题均可用此结论解决.运用如图1,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.小方同学在解答此题时,利用了上述结论,她的方法如下:连接CF并延长,交AB于点M,∵△ABC的高AD与高BE相交于点F,∴CM为△ABC的高.(请你在下面的空白处完成小方的证明过程.)
操作如图2,AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.
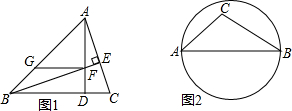
操作如图2,AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.

考点:作图—复杂作图
专题:
分析:首先根据在Rt△ADB中,AD=BD,则在Rt△BCM中,∠MBC=45°,进而得出CD=DF,AF=FG,即可得出答案,分别延长BC,AC分别交⊙O于点D,E,分别延长AD,BE交于点F,连接FC并延长到AB于点G,即可得出答案.
解答: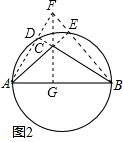
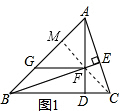 证明:如图1,连接CF并延长,交AB于点M,
证明:如图1,连接CF并延长,交AB于点M,
在Rt△ADB中,AD=BD,
∵在Rt△BCM中,∠MBC=45°,
∴∠BCM=45°,即∠DCF=45°,
∴在Rt△CFD中,CD=DF,
∵FG∥BC,∴∠AGF=∠ABC=45°,
∴在Rt△AFG中,AF=FG,
∴FG+CD=AF+DF=AD=BD;
如图2,CG即为△ABC中AB边上的高.

 证明:如图1,连接CF并延长,交AB于点M,
证明:如图1,连接CF并延长,交AB于点M,在Rt△ADB中,AD=BD,
∵在Rt△BCM中,∠MBC=45°,
∴∠BCM=45°,即∠DCF=45°,
∴在Rt△CFD中,CD=DF,
∵FG∥BC,∴∠AGF=∠ABC=45°,
∴在Rt△AFG中,AF=FG,
∴FG+CD=AF+DF=AD=BD;
如图2,CG即为△ABC中AB边上的高.
点评:此题主要考查了复杂作图以及等腰直角三角形的性质等知识,根据圆周角定理得出G点位置是解题关键.

练习册系列答案
相关题目
二次函数y=2(x+1)2-3的最小值是( )
| A、1 | B、-1 | C、3 | D、-3 |
若抛物线y=(x-2m)2+3m-1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是( )
| A、m<2 | ||
| B、m>2 | ||
C、m<
| ||
D、m>
|
 如图,在△ABC中,点D、E分别为边AB、AC上的点,且DE∥BC,若AD=5,BD=10,AE=3,则CE的长为( )
如图,在△ABC中,点D、E分别为边AB、AC上的点,且DE∥BC,若AD=5,BD=10,AE=3,则CE的长为( ) 在学习了几何中的对称知识以后,拉拉忽然想起了以前做过的一道题:有一组数排成方阵,如图,试计算这组数的和.拉拉想,方阵就像正方形,正方形是轴对称图形,也是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题呢?拉拉试了试,竟得到了非常巧妙的方法.你也来试试看.
在学习了几何中的对称知识以后,拉拉忽然想起了以前做过的一道题:有一组数排成方阵,如图,试计算这组数的和.拉拉想,方阵就像正方形,正方形是轴对称图形,也是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题呢?拉拉试了试,竟得到了非常巧妙的方法.你也来试试看.