Question

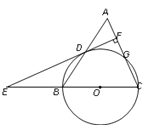
【题目】如图，等腰三角形ABC中，AC＝BC＝10，AB＝12. 以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E.

(1)求证：直线EF是⊙O的切线；

(2)求sin∠E的值.

Answer 1

【答案】(1)证明见解析；(2).

【解析】

（1）求证直线EF是⊙O的切线，只要连接OD证明OD⊥EF即可；
（2）根据∠E=∠CBG，可以把求sin∠E的值得问题转化为求sin∠CBG，进而转化为求Rt△BCG中，两边的比的问题．

(1)连结OD, CD.

∵BC是直径,

∴CD⊥AB.

∵AC=BC,

∴D是AB的中点.

又O为BC中点,

∴OD∥AC.

∵DF⊥AC,

∴OD⊥EF.

∴直线EF是⊙O的切线.

(2)连结BG.

∵BC是直径,

∴∠BGC=90°.

在Rt△BCD中, CD=.

∵AB·CD=AC·BG,

∴BG=.

在Rt△BGC中， CG=.

∵BG∥EF,

∴∠E=∠CBG.

∴sin∠E=sin∠CBG=.