题目内容
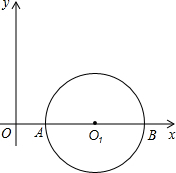
已知:半径为1的⊙O1与x轴交于A、B两点,圆心O1的坐标为(2,0),二次函数y=-x2+b x+c的图象经过A、B两点,其顶点为F.
x+c的图象经过A、B两点,其顶点为F.
(1)求b、c的值及二次函数顶点F的坐标;
(2)写出将二次函数y=-x2+bx+c的图象向下平移1个单位再向左平移2个单位的图象的函数表达式;
(3)经过原点O的直线l与⊙O相切,求直线l的函数表达式.
 解:(1)由已知得:A(1,0),B(3,0)
解:(1)由已知得:A(1,0),B(3,0)由题意:

解得:
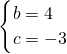
∴y=-x2+4x-3=-(x-2)2+1
∴顶点F(2,1)
(2)y=-x2
(3)设经过原点O的直线l:y=kx(k≠0)与⊙O1相切于点C
则O1C⊥OC,OO1=2,O1C=1
∴OC=
 ,∠O1OC=30°
,∠O1OC=30°设点C的坐标为(xc,yc)
则
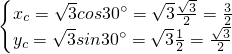
∴
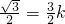 ,得
,得
∴y=
 x
x由圆的对称性,另一条直线l的解析式是y=-
 x.
x.分析:(1)根据⊙O1的半径和圆心的坐标,可求得A、B两点的坐标,然后将它们代入抛物线的解析式中,可求出b、c的值.进而可根据二次函数的解析式求出顶点F的坐标.
(2)将原抛物线的解析式化为顶点式,然后再按题目给出的步骤,一步一步的进行平移.
(3)过原点的直线是正比例函数,只需求得直线与圆的切点的坐标,即可确定直线l的解析式.(根据圆的对称性可知,符合条件的直线l应该有两条)
点评:本题主要考查了函数解析式的确定、切线的性质、二次函数图象的平移等知识.综合性强,难度较大.

练习册系列答案
相关题目
已知在半径为2的⊙O中,圆内接△ABC的边AB=2
,则∠C的度数为( )
| 3 |
| A、60° |
| B、30° |
| C、60°或120° |
| D、30°或150° |
 x+c的图象经过A、B两点,其顶点为F.
x+c的图象经过A、B两点,其顶点为F.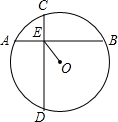 如图,已知在半径为2的⊙O中有一点E,过点E的弦AB与CD互相垂直,且OE=1,则AB2+CD2的值等于
如图,已知在半径为2的⊙O中有一点E,过点E的弦AB与CD互相垂直,且OE=1,则AB2+CD2的值等于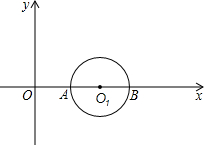 (2013•房山区一模)已知:半径为1的⊙O1与x轴交A、B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A、B两点,与y轴交于点C
(2013•房山区一模)已知:半径为1的⊙O1与x轴交A、B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A、B两点,与y轴交于点C