题目内容
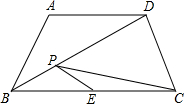 如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )
如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )| A、2 | ||
B、2
| ||
C、2
| ||
| D、3 |
考点:轴对称-最短路线问题,等腰梯形的性质
专题:
分析:根据等腰梯形的性质,得出BC的长度,作出E关于BD的对称点E′,转化为线段长度的问题,再根据等边三角形的性质判断出△ABE′为等边三角形,利用勾股定理即可求出CE′的长.
解答: 解:过点A作AF⊥BC于点F,连接AE,AC交BD于点P,
解:过点A作AF⊥BC于点F,连接AE,AC交BD于点P,
∵在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,
∴∠ABC=60°,
∴∠BAF=30°,
∴BF=
AB=1,AF=
=
,FC=3,
同理可得出:BC=AD+2=4,
∵BD是∠ABC的平分线.
作E关BD的对称点E′与A点重合,
则PE=PE′,
此时,PE+PC=PE′+PC=CE′,
CE′即为PE+PC的最小值.
∵∠ABC=60°,
又∵BE′=BE,
∴△E′BE为正三角形,EE′=2,∠ABE=60°,
故EE′=EC,
∠EE′C=∠ECE′=30°,
∴∠BE′C=60°+30°=90°,
在Rt△BCE′中,
CE′=
=2
.
故选;C.
 解:过点A作AF⊥BC于点F,连接AE,AC交BD于点P,
解:过点A作AF⊥BC于点F,连接AE,AC交BD于点P,∵在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,
∴∠ABC=60°,
∴∠BAF=30°,
∴BF=
| 1 |
| 2 |
| 22-12 |
| 3 |
同理可得出:BC=AD+2=4,
∵BD是∠ABC的平分线.
作E关BD的对称点E′与A点重合,
则PE=PE′,
此时,PE+PC=PE′+PC=CE′,
CE′即为PE+PC的最小值.
∵∠ABC=60°,
又∵BE′=BE,
∴△E′BE为正三角形,EE′=2,∠ABE=60°,
故EE′=EC,
∠EE′C=∠ECE′=30°,
∴∠BE′C=60°+30°=90°,
在Rt△BCE′中,
CE′=
(
|
| 3 |
故选;C.
点评:此题考查了轴对称---最短路径问题,内容涉及等腰梯形的性质、等边三角形的性质和判定及勾股定理,综合性较强.

练习册系列答案
相关题目
某种鲸的体重可达136 000 000克,用科学记数法表示数据136 000 000是( )
| A、13.6×107 |
| B、136×106 |
| C、1.36×107 |
| D、1.36×108 |
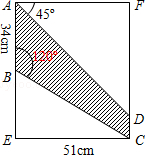 丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算:
丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算: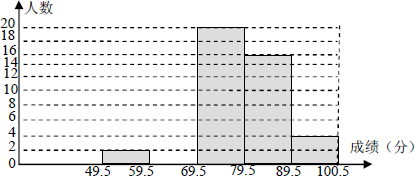
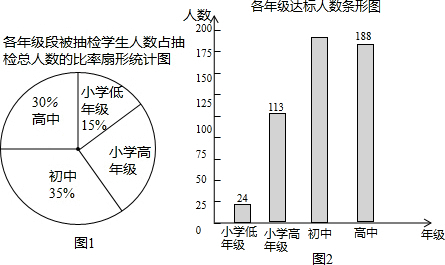
 为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每月评分制,现对初一上期1-5学月的评分情况进行统计,其中学生小明5次得分情况如下表所示:
为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每月评分制,现对初一上期1-5学月的评分情况进行统计,其中学生小明5次得分情况如下表所示: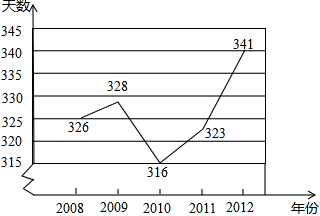 宁波市努力改造空气质量,根据宁波市环境保护局公布的2008-2012这五年各年的全年空气质量优良的天数,绘制折线图如图,根据图中的信息回答:
宁波市努力改造空气质量,根据宁波市环境保护局公布的2008-2012这五年各年的全年空气质量优良的天数,绘制折线图如图,根据图中的信息回答: