题目内容
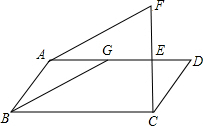 (2008•上海模拟)已知:如图,点E、G在平行四边形ABCD的边AD上,EG=ED,延长CE到点F,使得EF=EC.求证:AF∥BG.
(2008•上海模拟)已知:如图,点E、G在平行四边形ABCD的边AD上,EG=ED,延长CE到点F,使得EF=EC.求证:AF∥BG.分析:连接FG,FD,GC,利用对角线互相平分的四边形是平行四边形判定四边形FGCD是平行四边形,然后根据平行四边形的对边平行且相等可得FG∥DC,FG=DC,又四边形ABCD也是平行四边形,所以AB∥DC,AB=DC,从而得到AB∥FG,AB=FG,然后得到四边形ABGF是平行四边形,根据平行四边形的对边平行即可得证.
解答:证明: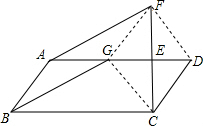 连接FG,FD,GC.
连接FG,FD,GC.
∵EG=ED,EF=EC,
∴四边形FGCD是平行四边形(对角线互相平分的四边形是平行四边形),
∴FG∥DC,FG=DC(平行四边形对边相等且平行),
∵平行四边形ABCD,
∴AB∥DC,AB=DC,
∴AB∥FG,AB=FG,
∴四边形ABGF是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴AF∥BG.
 连接FG,FD,GC.
连接FG,FD,GC.∵EG=ED,EF=EC,
∴四边形FGCD是平行四边形(对角线互相平分的四边形是平行四边形),
∴FG∥DC,FG=DC(平行四边形对边相等且平行),
∵平行四边形ABCD,
∴AB∥DC,AB=DC,
∴AB∥FG,AB=FG,
∴四边形ABGF是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴AF∥BG.
点评:本题考查了平行四边形的判定与性质,主要利用了对角线互相平分的四边形是平行四边形,一组对边平行且相等的四边形是平行四边形,平行四边形的对边平行且相等,作出辅助线构造出平行四边形是解题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
