题目内容
【题目】如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?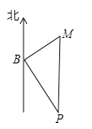
【答案】解:BM=8×2=16海里,
BP=15×2=30海里,
在△BMP中,BM2+BP2=256+900=1156,PM2=1156,
BM2+BP2=PM2 ,
∴∠MBP=90°,
180°﹣90°﹣60°=30°,
故乙船沿南偏东30°方向航行.
【解析】先根据路程=速度×时间,求出BM,BP的长,再根据勾股定理的逆定理得到∠MBP=90°,进一步即可求解.
【考点精析】掌握勾股定理的逆定理和关于方向角问题是解答本题的根本,需要知道如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.

练习册系列答案
相关题目