Question

【题目】阅读下列材料：

数学课上，老师出示了这样一个问题：

如图1，正方形为中，点、在对角线上，且，探究线段、、之间的数量关系，并证明.

某学习小组的同学经过思考，交流了自己的想法：

小明：“通过观察和度量，发现与存在某种数量关系”；

小强：“通过观察和度量，发现图1中线段与相等”；

小伟：“通过构造（如图2），证明三角形全等，进而可以得到线段、、之间的数量关系”.

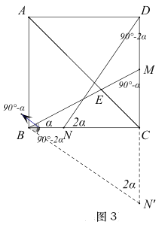
老师：“此题可以修改为‘正方形中，点在对角线上，延长交于点，在上取一点，连接（如图3）.如果给出、的数量关系与、的数量关系，那么可以求出的值”.

请回答：

（1）求证：；

（2）探究线段、、之间的数量关系，并证明；

（3）若，，求的值（用含的代数式表示）.

Answer 1

【答案】（1）详见解析；（2），证明详见解析；（3）

【解析】

(1)依题意由SAS可证：.可推

（2）过点作，且，连接、，由SAS可证

可得，可得.利用勾股定理即可知：.即.

（3）延长至使，连接.设，，

则，，，，.由SAS可证，可得 ，，由角关系推出.

所以.推出，所以.得出结论.

（1）证明：∵四边形为正方形，

∴，.

∵，

∴.

∴.

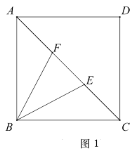
（2）结论：.

证明：如图2，过点作，且，连接、，

则，.

∵，，

∴

∴，.

∴.

∴.

即.

（3）解：延长至使，连接.

设，，

则，，.

∵四边形为正方形，

∴，，

，.

∴，

∴，，

.

∴.

∴.

∴.

∴.