题目内容
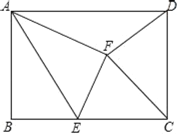
【题目】如图,在矩形ABCD中,点E是BC边上的一个动点,沿着AE翻折矩形,使点B落在点F处若AB=3,BC=![]() AB,解答下列问题:
AB,解答下列问题:
(1)在点E从点B运动到点C的过程中,求点F运动的路径长;
(2)当点E是BC的中点时,试判断FC与AE的位置关系,并说明你的理由;
(3)当点F在矩形ABCD内部且DF=CD时,求BE的长.
【答案】(1)2π;(2)FC与AE的位置关系为:FC∥AE;(3)![]()
【解析】
(1)根据翻折的性质可得AF=AB,∠BAE=∠EAF,当当点E运动到点C时利用三角函数求出∠BAF的度数,最后再根据弧长公式,求出点F的运动路径长.(2)根据题意知道BE=EF=EC,再利用三角形内角和∠BFE+∠CFE=90°,最后根据翻折的性质求出∠BHE=90°,即可证出FC与AE的位置关系.(3) 过点F作FM⊥AD于点M,延长MF交BC于点N,根据题意求出AM的值,然后利用勾股定理求出MF,根据矩形的性质得到FN, 设BE=x,则EN=![]() ﹣x,利用勾股定理求出BE的长.
﹣x,利用勾股定理求出BE的长.
解:(1)由翻折的性质得:AF=AB,∠BAE=∠EAF,
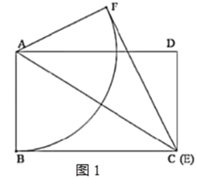
∴点F运动的路径是以A为圆心,AB为半径,∠BAF为圆心角的弧长,如图1所示:
当点E运动到点C时,tan∠BAE=![]() =
=![]()
∴∠BAE=60°,∠BAF=120°,
∴点F的运动路径长为:![]() =2π;
=2π;
(2)FC与AE的位置关系为:FC∥AE;理由如下:
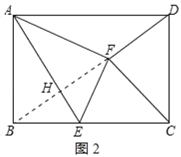
连接BF交AE于点H,如图2所示:
由折叠性质得:BE=EF,
∵BE=CE,
∴BE=EF=EC,
∴∠FBE=∠BFE,∠CFE=∠FCE,
∵∠FBE+∠BFE+∠CFE+∠FCE=180°,
∴∠BFE+∠CFE=90°,即∠BFC=90°,
由折叠的性质得:BF⊥AE,
∴∠BHE=90°,
∴FC∥AE;
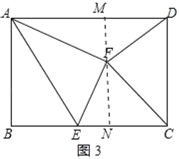
(3)过点F作FM⊥AD于点M,延长MF交BC于点N,如图3所示:
∵AB=3,BC=![]() AB,
AB,
∴BC=3![]() ,
,
∵四边形ABCD是矩形,
∴AB=CD=3,DF=DC=3,
∴AF=DF,
∵MF⊥AD,
∴AM=![]() AD=
AD=![]()
在Rt△MAF中,MF=![]() =
=![]() =
=![]() ,
,
∵∠BAD=∠B=90°,MF⊥AD,
∴四边形ABNM是矩形,
∴BN=AM=![]() ,MN=AB=3,
,MN=AB=3,
∴FN=MN﹣MF=3﹣![]() =
=![]() ,
,
设BE=x,则EN=![]() ﹣x,
﹣x,
由折叠的性质得:FE=BE=x,
在Rt△EFN中,EF2﹣EN2=FN2,
即:x2﹣(![]() ﹣x)2=(
﹣x)2=(![]() )2,
)2,
解得:x=![]() ,
,
∴BE的长为![]() .
.