题目内容
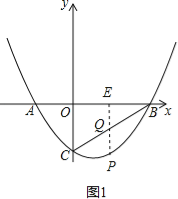
【题目】如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),且tan∠ABC=![]() .
.
(1)求抛物线的解折式.
(2)在直线BC下方抛物线上一点P,当四边形OCPB的面积取得最大值时,求此时点P的坐标.
(3)在y轴的左侧抛物线上有一点M,满足∠MBA=∠ABC,若点N是直线BC上一点,当△MNB为等腰三角形时,求点N的坐标.

【答案】(1)抛物线的解折式为y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)P点的坐标为(![]() ,﹣
,﹣![]() );
);
(3)点N的坐标为(﹣2,﹣ ![]() )或(8,
)或(8, ![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)由解析式求得C的坐标,然后根据tan∠ABC=![]() 求得OB=3,从而求得B的坐标,进而根据待定系数法即可求得解析式;
求得OB=3,从而求得B的坐标,进而根据待定系数法即可求得解析式;
(2)过点P作y轴的平行线与BC交于点Q,与OB交于点E,设P(x,x2﹣2x﹣3),易得,直线BC的解析式为y=x﹣3则Q点的坐标为(x,x﹣3),再根据S四边形ABPC=S△ABC+S△BPQ+S△CPQ即可得出结论.
(3)根据题意求得M的坐标,然后分三种情况讨论求得即可.
解:(1)由抛物线y=ax2+bx﹣2可知C的坐标为(0,﹣2),
∴OC=2,
∵tan∠ABC=![]() =
=![]()
∴OB=3,
∴B(3,0),
∵A(﹣1,0),
把A、B的坐标代入y=ax2+bx﹣2得:
![]()
解得 ,
,
∴抛物线的解折式为y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)过点P作y轴的平行线与BC交于点Q,与OB交于点E,
设P(x,![]() x2﹣
x2﹣![]() x﹣2),
x﹣2),
设直线BC的解析式为y=kx+b(k≠0),
∵B(3,0),C(0,﹣2),
∴![]() ,
,
解得 ,
,
∴直线BC的解析式为y=![]() x﹣2.
x﹣2.
∴Q点的坐标为(x,![]() x﹣2),
x﹣2),
∴S四边形ABPC=S△ABC+S△BPQ+S△CPQ
=![]() ABOC+
ABOC+![]() QPOE+
QPOE+![]() QPEB
QPEB
=![]() ×4×2+
×4×2+![]() (2x﹣
(2x﹣![]() x2)×3
x2)×3
=﹣x2+3x+4
=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,四边形ABPC的面积最大,最大面积为
时,四边形ABPC的面积最大,最大面积为![]() .此时P点的坐标为(
.此时P点的坐标为(![]() ,﹣
,﹣![]() ).
).
(3)设直线AM交y轴于D,
∵∠MBA=∠ABC,
∴OD=OC=2,
∴D(0,2),
设直线AM的解析式为y=mx+2,
代入B(3,0)得0=3m+2,解得m=﹣![]() ,
,
∴直线AM的解析式为y=﹣![]() x+2,
x+2,
解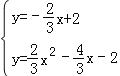 得
得 或
或![]() ,
,
∴M(﹣2,![]() ),
),
设N(x,![]() x﹣2),
x﹣2),
∵BM2=(3+2)2+(![]() )2,MN2=(x+2)2+(
)2,MN2=(x+2)2+(![]() x﹣2﹣
x﹣2﹣![]() )2,BN2=(x﹣3)2+(
)2,BN2=(x﹣3)2+(![]() x﹣2)2,
x﹣2)2,
当MB=BN时,N(﹣2,﹣![]() )或(8,
)或(8,![]() );
);
当MB=MN时,则(3+2)2+(![]() )2=(x+2)2+(
)2=(x+2)2+(![]() x﹣2﹣
x﹣2﹣![]() )2,
)2,
整理得13x2﹣28x﹣33=0,
解得x1=3,x2=﹣![]() ,
,
∴N(﹣![]() ,﹣
,﹣![]() );
);
当BN=MN时,(x+2)2+(![]() x﹣2﹣
x﹣2﹣![]() )2=(x﹣3)2+(
)2=(x﹣3)2+(![]() x﹣2)2,
x﹣2)2,
整理得10x=﹣35,
解得x=﹣![]()
∴N(﹣![]() ,﹣
,﹣![]() );
);
综上,点N的坐标为(﹣2,﹣![]() )或(8,
)或(8,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).