题目内容
【题目】如图，抛物线y=﹣ 
x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．
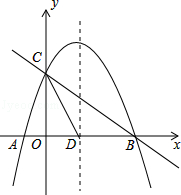
（1）求抛物线的表达式；
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．
【答案】
（1）
解：把A（﹣1，0），C（0，2）代入y=﹣ 
x2+mx+n得 
，解得 
，
∴抛物线解析式为y=﹣ x2+ 
x+2
（2）
解：存在．
抛物线的对称轴为直线x=﹣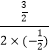 
= ，
则D（ ，0），
∴CD= 
= 
= 
，
如图1，当CP=CD时，则P1（ ，4）；
当DP=DC时，则P2（ ， ），P3（ ，﹣ ），
综上所述，满足条件的P点坐标为（ ，4）或（ ， ）或（ ，﹣ ） 
（3）
解：当y=0时，=﹣ x2+ x+2=0，解得x1=﹣1，x2=4，则B（4，0），
设直线BC的解析式为y=kx+b，
把B（4，0），C（0，2）代入得 
，解得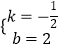 
，
C的解析式为y=﹣ x+2，
设E（x，﹣ x+2）（0≤x≤4），则F（x，﹣ x2+ x+2），
∴FE=﹣ x2+ x+2﹣（﹣ x+2）=﹣ x2+2x，
∵S△BCF=S△BEF+S△CEF= 4EF=2（﹣ x2+2x）=﹣x2+4x，
而S△BCD= ×2×（4﹣ ）= ，
∴S四边形CDBF=S△BCF+S△BCD
=﹣x2+4x+ （0≤x≤4），
=﹣（x﹣2）2+ 
.
当x=2时，S四边形CDBF有最大值，最大值为 . ，此时E点坐标为（2，1）
【解析】（1）直接把A点和C点坐标代入y=﹣ x2+mx+n得m、n的方程组，然后解方程组求出m、n即可得到抛物线解析式；（2）先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣ ，则D（ ，0），则利用勾股定理计算出CD= ，然后分类讨论：如图1，当CP=CD时，利用等腰三角形的性质易得P1（ ，4）；当DP=DC时，易得P2（ ， ），P3（ ，﹣ ）；（3）先根据抛物线与x轴的交点问题求出B（4，0），再利用待定系数法求出直线BC的解析式为y=﹣ x+2，利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征，设E（x，﹣ x+2）（0≤x≤4），则F（x，﹣ x2+ x+2），则FE=﹣ x2+2x，由于△BEF和△CEF共底边，高的和为4，则S△BCF=S△BEF+S△CEF= 4EF=﹣x2+4x，加上S△BCD= ，所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+ （0≤x≤4），然后根据二次函数的性质求四边形CDBF的面积最大，并得到此时E点坐标．
