题目内容
【题目】如图,在矩形ABCD中,AB=10,动点E、F分别在边AB、AD上,且AF=![]() AE.将△AEF绕点E顺时针旋转90°得到△A'EF',设AE=x,△A'EF'与矩形ABCD重叠部分面积为S,S的最大值为9.
AE.将△AEF绕点E顺时针旋转90°得到△A'EF',设AE=x,△A'EF'与矩形ABCD重叠部分面积为S,S的最大值为9.
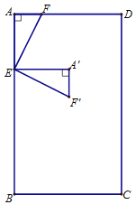
(1)求AD的长;
(2)求S关于x的函数解析式,并写出自变量x的取值范围.
【答案】(1)![]() ;(2)
;(2)
【解析】
(1)根据题意,当![]() 在
在![]() 上时,
上时,![]() ,则重叠的面积有最大值9,根据面积公式,即可求出AD的长度
,则重叠的面积有最大值9,根据面积公式,即可求出AD的长度
(2)根据题意,需要对x的值进行讨论分析,分成三种情况进行解题,分别求出S与x的关系式,即可得到答案.
(1)如图,当![]() 在
在![]() 上时,
上时,![]() ,
,
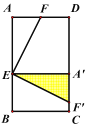
∵![]() ,
,![]() ,
,
∴![]() .
.
解方程,得:![]() 或
或![]() (舍去),
(舍去),
∴![]() .
.
(2)①当![]() 时,如图,
时,如图,

![]() .
.
②如图可知,![]() 经过点
经过点![]() 时,
时,![]() ,
,

![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
当![]() 时,如图,
时,如图,![]() ,
,
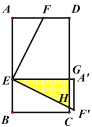
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
③当![]() 时,如图,
时,如图,![]() ,
,![]() ,
,

在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
∵![]() 矩形
矩形![]() ,
,
![]() .
.
综上所述: .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图

根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?