题目内容
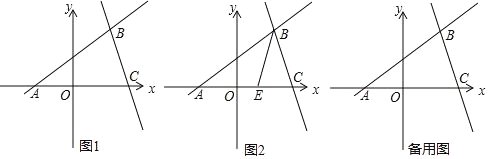
【题目】如图,抛物线y=nx2﹣3nx﹣4n(n<0)与x轴交于B、C两点(点B在点C的左侧),且抛物线与y轴交于点A.
(1)点B的坐标为 ,点C的坐标为 ;
(2)若∠BAC=90°,求抛物线的解析式.
(3)点M是(2)中抛物线上的动点,点N是其对称轴上的动点,是否存在这样的点M、N,使得以A、C、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

【答案】(1)(﹣1,0),(4,0);(2)y=﹣![]() x2+
x2+![]() x+2;(3)点M的坐标分别为:(﹣
x+2;(3)点M的坐标分别为:(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用x轴上点的坐标特点即可得出结论;
(2)判断出△AOB∽△COA,建立方程求出OA,进而得出点A坐标,最后用待定系数法即可的结论;
(3)设出点M,N的坐标,分三种情况,利用中点坐标公式建立方程求解即可得出结论.
(1)令y=0,
∴nx2-3nx-4n=0,
∵n<0,
∴x2-2x-4=0,
∴x=-1或x=4,
∴B(-1,0),C(4,0);
(2)∵∠BAC=90°,AO⊥BC,
易证△AOB~△COA,
∴![]() ,
,![]() ,
,
∴OA=2,
故A(0,2),
则设抛物线的解析式为:y=a(x-x1)( x-x2),
把A(0,2)、B(-1,0)、C(4,0)代入上式得,-4a=2,
∴![]() ,
,
∴![]() ,
,
∴对称轴直线为![]() ,
,
∴设N(![]() ,b),M(m,
,b),M(m,![]() ),
),
以A、C、M、N为顶点的四边形是平行四边形,
∴①当AC为对角线时,![]() ,
,
∴![]() .
.
∴M(![]() ,
,![]() ).
).
②当AM为对角线时,![]() ,
,
∴![]() .
.
∴M(![]() ,-
,-![]() ).
).
③当AN为对角线时,![]() ,
,
∴![]() .
.
∴M(![]() ,-
,-![]() ).
).
即:抛物线上存在这样的点M,点M的坐标分别为:M(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() )或(
)或(![]() ,-
,-![]() ).
).

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目