��Ŀ����
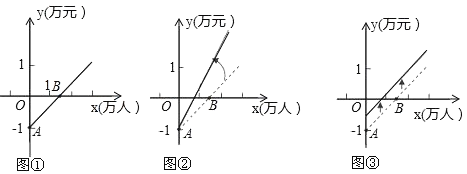
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��BC��![]() ��ֱ��BD��x�ύ�ڵ�A����B��2��3������D��0��
��ֱ��BD��x�ύ�ڵ�A����B��2��3������D��0��![]() ����
����
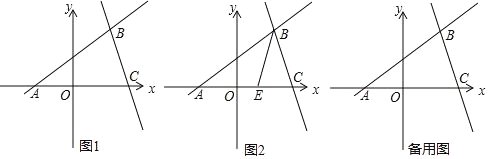
��1����ֱ��BD�ĺ�������ʽ��
��2����y������һ��P��ʹ�á�ABC���ACP�������ȣ������P�����ꣻ
��3����ͼ2��EΪ�߶�AC��һ�㣬����BE��һ����F�ӵ�B���������߶�BE��ÿ��1����λ�˶�����E�����߶�EA��ÿ��![]() ����λ�˶���A��ֹͣ�����F�������˶�����������ʱ��Ϊt����t����Сֵ��
����λ�˶���A��ֹͣ�����F�������˶�����������ʱ��Ϊt����t����Сֵ��
���𰸡���1��y=![]() x+
x+![]() ����2��P��0��3����0��-3������3��
����2��P��0��3����0��-3������3��![]()
��������
��1����ֱ��BD�Ľ���ʽy=kx+b����B��2��3����D��0��![]() ��������룬���ô���ϵ�����������
��������룬���ô���ϵ�����������
��2��������ABC����ACP�������ȣ��ó�P��������ľ���ֵ���ٸ��ݵ�P��y���ϣ��Ӷ�ȷ����P������
��3����������ɵ�![]() ������A����б��Ϊ45�ȵ�ֱ��l2������E��EF��l2���ڵ�F����B��E��F���㹲���Ҵ�ֱ��ֱ��l2ʱ��t��С����t=BF���������ֱ��l2��ֱ��BF�Ľ��㣬�Ӷ����F�������꣬�̶����BF�����ɣ�
������A����б��Ϊ45�ȵ�ֱ��l2������E��EF��l2���ڵ�F����B��E��F���㹲���Ҵ�ֱ��ֱ��l2ʱ��t��С����t=BF���������ֱ��l2��ֱ��BF�Ľ��㣬�Ӷ����F�������꣬�̶����BF�����ɣ�
�⣺��1����ֱ��BD�Ľ���ʽΪ��y=kx+b��
�� B��2��3����D��0��![]() ������������ʽ
������������ʽ
�ã� ��ã�
��ã�![]()
��ֱ��BD�ı���ʽΪ��y=![]() x+
x+![]() ��
��
��2������ABC����ACP��������
����ABC����ACPͬ�ף�
��![]()
�ߵ�P��y���ϣ�
��![]()
��P��0��3����0��-3��
��3����������ɵã�![]()
����A����б��Ϊ45�ȵ�ֱ��l2������E��EF��l2���ڵ�F��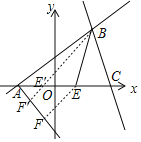
��EF=![]() AE����t=BE+EF��
AE����t=BE+EF��
��B��E��F���㹲���Ҵ�ֱ��ֱ��l2ʱ��t��С������t=![]() ����
����
ֱ��l2�ı���ʽΪ��y=-x-2��ֱ��BF����ʽΪ��y=x+1��
��������������ʽ��������ã�![]() ������F��
������F��![]()
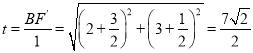 s
s