题目内容
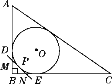
【题目】如图,点P在正方形ABCD边AD上,连接PB,过点B作一条射线与边DC的延长线交于点 Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ,若PQ=PB+PD+3,则△PAB的面积为____.

【答案】![]()
【解析】
设正方形的边长AB=a,PA=x,首先由∠QBE=∠PBC,∠QBE+∠QBC=90°易得△PAB与△QCB均为直角三角形,再证得△PAB≌△QCB,可知QC=PA,利用方程思想和勾股定理,等量代换易得ax,可得结果.
设正方形的边长AB=a,PA=x,
∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
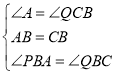 ,
,
∴△PAB≌△QCB(ASA),
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+3,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+3,
解得:2ax=3,
∴ax=![]() ,
,
∵S△PAB =![]() PAPB=
PAPB=![]() ax=
ax=![]()
![]() ,
,
故答案为:![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目