题目内容
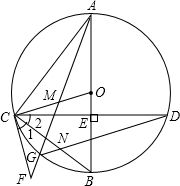 (2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=
| 1 | 4 |
分析:(1)根据切线的判定定理得出∠1+∠BCO=90°,即可得出答案;
(2)利用已知得出∠3=∠2,∠4=∠D,再利用相似三角形的判定方法得出即可;
(3)根据已知得出OE的长,进而利用勾股定理得出EC,AC,BC的长,即可得出CD,利用(2)中相似三角形的性质得出NB的长即可.
(2)利用已知得出∠3=∠2,∠4=∠D,再利用相似三角形的判定方法得出即可;
(3)根据已知得出OE的长,进而利用勾股定理得出EC,AC,BC的长,即可得出CD,利用(2)中相似三角形的性质得出NB的长即可.
解答: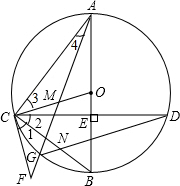 (1)证明:∵△BCO中,BO=CO,
(1)证明:∵△BCO中,BO=CO,
∴∠B=∠BCO,
在Rt△BCE中,∠2+∠B=90°,
又∵∠1=∠2,
∴∠1+∠BCO=90°,
即∠FCO=90°,
∴CF是⊙O的切线;
(2)证明:∵AB是⊙O直径,
∴∠ACB=∠FCO=90°,
∴∠ACB-∠BCO=∠FCO-∠BCO,
即∠3=∠1,
∴∠3=∠2,
∵∠4=∠D,
∴△ACM∽△DCN;
(3)解:∵⊙O的半径为4,即AO=CO=BO=4,
在Rt△COE中,cos∠BOC=
,
∴OE=CO•cos∠BOC=4×
=1,
由此可得:BE=3,AE=5,由勾股定理可得:
CE=
=
=
,
AC=
=
=2
,
BC=
=
=2
,
∵AB是⊙O直径,AB⊥CD,
∴由垂径定理得:CD=2CE=2
,
∵△ACM∽△DCN,
∴
=
,
∵点M是CO的中点,CM=
AO=
×4=2,
∴CN=
=
=
,
∴BN=BC-CN=2
-
=
.
 (1)证明:∵△BCO中,BO=CO,
(1)证明:∵△BCO中,BO=CO,∴∠B=∠BCO,
在Rt△BCE中,∠2+∠B=90°,
又∵∠1=∠2,
∴∠1+∠BCO=90°,
即∠FCO=90°,
∴CF是⊙O的切线;
(2)证明:∵AB是⊙O直径,
∴∠ACB=∠FCO=90°,
∴∠ACB-∠BCO=∠FCO-∠BCO,
即∠3=∠1,
∴∠3=∠2,
∵∠4=∠D,
∴△ACM∽△DCN;
(3)解:∵⊙O的半径为4,即AO=CO=BO=4,
在Rt△COE中,cos∠BOC=
| 1 |
| 4 |
∴OE=CO•cos∠BOC=4×
| 1 |
| 4 |
由此可得:BE=3,AE=5,由勾股定理可得:
CE=
| CO2-EO2 |
| 42-12 |
| 15 |
AC=
| CE2+AE2 |
(
|
| 10 |
BC=
| CE2+BE2 |
(
|
| 6 |
∵AB是⊙O直径,AB⊥CD,
∴由垂径定理得:CD=2CE=2
| 15 |
∵△ACM∽△DCN,
∴
| CM |
| CN |
| AC |
| CD |
∵点M是CO的中点,CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴CN=
| CM•CD |
| AC |
2×2
| ||
2
|
| 6 |
∴BN=BC-CN=2
| 6 |
| 6 |
| 6 |
点评:此题主要考查了相似三角形的判定与性质以及切线的判定和勾股定理的应用等知识,根据已知得出△ACM∽△DCN是解题关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 (2013•遂宁)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
(2013•遂宁)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于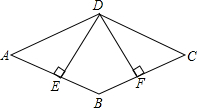 (2013•遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证:
(2013•遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证: (2013•遂宁)如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是
(2013•遂宁)如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 (2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是
(2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是