题目内容
【题目】(1)求证:无论p为何值,方程(x-2)(x-3)-p2=0总有两个不相等的实数根.
(2)若方程(x-2)(x-3)-p2=0的两根为正整数,试求p的值.
【答案】(1)见解析;(2)0或-![]() 或
或![]()
【解析】
(1)要证明方程总有两个不相等的实数根,那么只要证明△>0即可;
(2)将方程(x-2)(x-3)-p2=0化简为x2-5x+6-p2=0,其两根为正整数,求出两根,根据两根之积等于6-p2求解即可.
(1)把方程(x-2)(x-3)-p2=0化为一般形式得:
x2-5x+6-p2=0
△=(-5)2-4×1×(6-p2)=4p2+1
对于任意实数p,p2≥0
∴△=4p2+1>0
∴无论p为何值,方程(x-2)(x-3)-p2=0总有两个不相等的实数根.
(2)解:方程(x-2)(x-3)-p2=0化简得:x2-5x+6-p2=0
设方程的两个实数根为a和b.
则:a+b=5. 因为方程(x-2)(x-3)-p2=0的两根为正整数,所以,方程的根有下列两种情形:
方程的两个实数根为1,4;此时ab=4
方程的两个实数根为2,3; 此时ab=6
∴当ab=4时,6-p2=4,解得:p=±![]() ;
;
当ab=6 时,6-p2=6,解得:p=0;
综上,方程(x-2)(x-3)-p2=0的两根为正整数,则p的值为0或-![]() 或
或![]() .
.

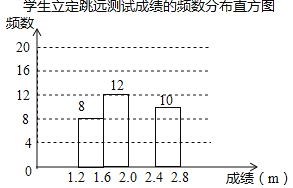
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?