Question

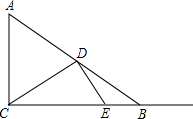（2014•静安区一模）如图，已知在Rt△ABC中，∠ACB=90°，AB=10，tanA=

4

3

，点D是斜边AB上的动点，联结CD，作DE⊥CD，交射线CB于点E，设AD=x．
（1）当点D是边AB的中点时，求线段DE的长；
（2）当△BED是等腰三角形时，求x的值；
（3）如果y=

DE

DB

，求y关于x的函数解析式，并写出它的定义域．

Answer 1

分析：（1）在直角三角形ABC中，由AB与tanA的值，利用锐角三角函数定义及勾股定理求出BC与AC的长，由D为斜边上的中点，利用直角三角形斜边上的中线等于斜边的一半得到CD=AD=BD=5，可得出∠DCB=∠DBC，再由一对直角相等，利用两对对应角相等的三角形相似得到三角形EDC与三角形ACE相似，由相似得比例，即可求出DE的长；
（2）分两种情况考虑：
（i）当E在BC边上时，由三角形BDE为等腰三角形且∠BED为钝角，得到DE=BE，利用等边对等角得到∠EBD=∠EDB，利用等角的余角相等得到∠CDA=∠A，利用等角对等边得到CD=AC，作CH垂直于AB，利用三线合一得到AD=2AH，由cosA的值求出AH的长，进而求出AD的长，即为x的值；
（ii）当E为BC延长线上时，与∠DBE为钝角得到DB=BE，同理求出x的值；
（3）作DM垂直于BC，得到DM与AC平行，由平行得比例，表示出DM与BM，进而表示出CD与CM，由三角形DEM与三角形CDM相似得比例，表示出DE，由BD=AB-AD=10-x，将DE与DB代入表示出y，化简得到结果，并求出x的范围即可．

解答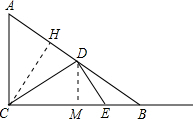：解：（1）在△ABC中，∵∠ACB=90°，AB=10，tanA=

4

3

，
∴BC=8，AC=6，
∵点D为斜边AB的中点，∴CD=AD=BD=5，
∴∠DCB=∠DBC，
∵∠EDC=∠ACB=90°，
∴△EDC∽△ACB，
∴

DE

CD

=

AC

BC

，即

DE

5

=

6

8

，
则DE=

15

4

；

（2）分两种情况情况：
（i）当E在BC边长时，
∵△BED为等腰三角形，∠BED为钝角，
∴EB=ED，
∴∠EBD=∠EDB，
∵∠EDC=∠ACB=90°，
∴∠CDA=∠A，
∴CD=AC，
作CH⊥AB，垂足为H，那么AD=2AH，
∴

AH

AC

=

3

5

，即AH=

18

5

，
∴AD=

36

5

，即x=

36

5

；
（ii）当E在CB延长线上时，
∵△BED为等腰三角形，∠DBE为钝角，
∴BD=DE，
∴∠BED=∠BDE，
∵∠EDC=90°，
∴∠BED+∠BCD=∠BDE+∠EDC=90°，
∴∠BCD=∠BDC，
∴BD=BC=8，
∴AD=x=AB-BD=10-8=2；

（3）作DM⊥BC，垂足为M，
∵DM∥AC，
∴

DM

AC

=

BM

BC

=

BD

BA

，
∴DM=

3

5

（10-x），BM=

4

5

（10-x），
∴CM=8-

4

5

（10-x）=

4

5

x，CD=

x2- 36 5 x+36

，
∵△DEM∽△CDM，
∴

DE

DM

=

CD

CM

，即DE=

DM•CD

CM

=

3(10-x)

4x

x2- 36 5 x+36

，
∴y=

DE

DB

=

3(10-x) 4x x2- 36 5 x+36

10-x

，
整理得：y=

3

20x

25x2-180x+900

（0＜x＜10）．

点评：此题属于相似型综合题，涉及的知识有：相似三角形的判定与性质，锐角三角函数定义，勾股定理，直角三角形斜边上的中线性质，等腰三角形的判定与性质，利用了分类讨论的思想，熟练掌握相似三角形的判定与性质是解本题的关键．