题目内容
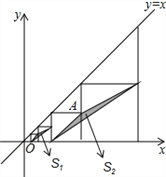
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
【答案】24n﹣5
【解析】∵函数y=x与x轴的夹角为45°,
∴直线y=x与正方形的边围成的三角形是等腰直角三角形.
∵A(8,4),
∴第四个正方形的边长为8,
第三个正方形的边长为4,
第二个正方形的边长为2,
第一个正方形的边长为1,
…,
第n个正方形的边长为2n﹣1.
由图可知,S1=![]() ×1×1+
×1×1+![]() ×(1+2)×2﹣
×(1+2)×2﹣![]() ×(1+2)×2=
×(1+2)×2=![]() ,
,
S2=![]() ×4×4+
×4×4+![]() ×(2+4)×4﹣
×(2+4)×4﹣![]() ×(2+4)×4=8,
×(2+4)×4=8,
…,
Sn为第2n与第2n﹣1个正方形中的阴影部分,
第2n个正方形的边长为22n﹣1,第2n﹣1个正方形的边长为22n﹣2,
∴Sn=![]() 22n﹣222n﹣2=24n﹣5.
22n﹣222n﹣2=24n﹣5.
故答案为:24n﹣5.
点晴:找规律问题是中考试卷中的热点问题,也是中考试卷中的难点所在,其难度大、区分度高,学生往往因找不到规律而无法解决此类问题,解决此类问题的关健是在于将变量(如正方形的边长)与序号联系在一起进行考虑,通过观察、分析、思考、建模从而建立起求阴影面积的计算模型.

练习册系列答案
相关题目