题目内容
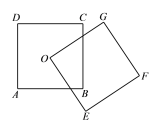
【题目】如图所示,正方形ABCD和正方形OEFG的边长均为5,O为正方形ABCD的中心,则图中重叠部分的面积是 _______.
【答案】![]()
【解析】
如图,连接OB、OC,根据正方形的对角线相等且互相平分可得OB=OC,再根据两角的和等于90°可以证明∠COH=∠BOG,又∠OBG=∠OCB=45°,证明△OBG与△OCH全等,从而得到重叠部分的面积等于△OBC的面积,即正方形的面积的![]() .
.
如图,连接OB、OC.
∵O为正方形ABCD的中心,∴OB=OC,∠OBG=∠OCB=45°.
∵∠COH+∠BOH=90°,∠BOG+∠BOH=90°,∴∠COH=∠BOG.
在△OBG与△OCH中,∵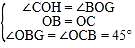 ,∴△OBG≌△OCH(ASA),∴S△OBG=S△OCH,∴重叠部分的面积=△OBC的面积
,∴△OBG≌△OCH(ASA),∴S△OBG=S△OCH,∴重叠部分的面积=△OBC的面积![]() S正方形ABCD.
S正方形ABCD.
∵S正方形ABCD=52=25,∴重叠部分的面积是![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目