题目内容
【题目】已知:如图,![]() ,
,![]() 分别为垂足,
分别为垂足,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
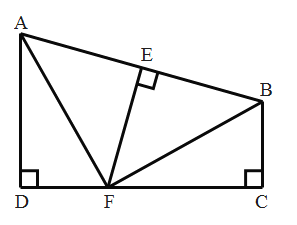
求证:(1)![]() ;(2)
;(2)![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据条件可以得出△ADF≌△FCB就可以得出∠DAF=∠CFB;
(2)根据∠DAF+DFA=90°可以得出∠AFB=90°,就可以得出△AFB是等腰直角三角形, 从而求解.
证明:(1)∵![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
∴AF=BF,AE=BE.
∵AD⊥CD,BC⊥CD,
∴∠D=∠C=90°.
在Rt△ADF和Rt△FCB中![]() ,
,
∴△ADF≌△FCB(HL),
∴∠DAF=∠CFB;
(2)∵∠D=90°,
∴∠DAF+∠DFA=90°,
∴∠CFB+∠DFA=90°,
∴∠AFB=90°.
∴![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目