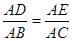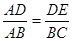题目内容
(本题满分10分)
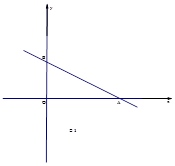
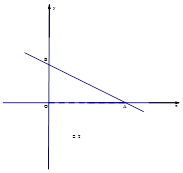
如图,在平面直角坐标系中,直线AB: 分别与x轴、y轴交于点A、B,
分别与x轴、y轴交于点A、B,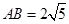 .
.
(1)求b的值.
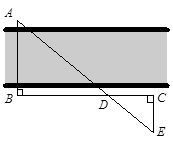
(2)动点C从A点出发以2个单位/秒的速度沿x轴的正半轴运动,动点D从B点出发以1个单位/秒的速度沿y轴的正半轴运动.运动时间为t(t>0),过A作x轴的垂线交直线CD于点P,过P作y轴的垂线交直线AB于点F,设线段BF的长为d(d>0),求d与t的函数关系式.
(3)在(2)的条件下,以点A为圆心,2为半径作⊙A,过点C作不经过第三象限的直线l与⊙A相切,切点为Q, 直线l与y轴交于点E,作QH⊥AE于H,交x轴于点G,是否存在t值,使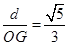 ,若存在,求出t值;若不存在,请说明理由.
,若存在,求出t值;若不存在,请说明理由.
如图,在平面直角坐标系中,直线AB:
 分别与x轴、y轴交于点A、B,
分别与x轴、y轴交于点A、B,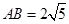 .
.

(1)求b的值.
(2)动点C从A点出发以2个单位/秒的速度沿x轴的正半轴运动,动点D从B点出发以1个单位/秒的速度沿y轴的正半轴运动.运动时间为t(t>0),过A作x轴的垂线交直线CD于点P,过P作y轴的垂线交直线AB于点F,设线段BF的长为d(d>0),求d与t的函数关系式.
(3)在(2)的条件下,以点A为圆心,2为半径作⊙A,过点C作不经过第三象限的直线l与⊙A相切,切点为Q, 直线l与y轴交于点E,作QH⊥AE于H,交x轴于点G,是否存在t值,使
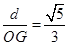 ,若存在,求出t值;若不存在,请说明理由.
,若存在,求出t值;若不存在,请说明理由.(1)b=2
(2)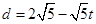 (0﹤t﹤2)
(0﹤t﹤2) 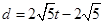 ( t>2),(3)t=3
( t>2),(3)t=3
(2)
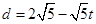 (0﹤t﹤2)
(0﹤t﹤2) 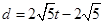 ( t>2),(3)t=3
( t>2),(3)t=3试题分析:(1)依题意知,直线AB:
 分别与x轴、y轴交于点A、B,所以B点为:当x=0时,y=b,A点为:当y=0时,x=2b。所以A(2b,0)B(0,b)。已知
分别与x轴、y轴交于点A、B,所以B点为:当x=0时,y=b,A点为:当y=0时,x=2b。所以A(2b,0)B(0,b)。已知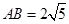
所以在Rt△AOB中,
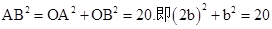 ,解得b=2(舍去-2)。
,解得b=2(舍去-2)。(2)依题意作图:
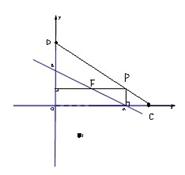 且BF=d(d>0),运动时间为t(t>0)。由(1)知,AB直线解析式为
且BF=d(d>0),运动时间为t(t>0)。由(1)知,AB直线解析式为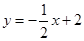 ,则F在AB上,y=AP=2t,此时x=4-4t。所以
,则F在AB上,y=AP=2t,此时x=4-4t。所以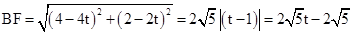 (t>0)
(t>0)所以
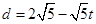 ,0﹤t﹤2。
,0﹤t﹤2。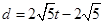 ( t>2)
( t>2)(3)依题意作图
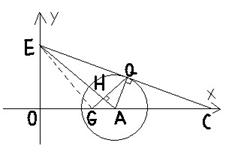
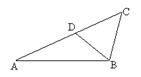
由图,易证△GAH∽△EAO(AAA)∴
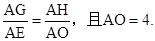 ∴4AG=AE·AH
∴4AG=AE·AH又∵△AHQ∽△AQE(AAA)可得

所以
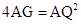 ,因为AQ=r=2,所以AG=1.OG=OA-AG=3.
,因为AQ=r=2,所以AG=1.OG=OA-AG=3.已知
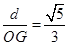 ,即3d=
,即3d=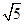 OG,3d=3
OG,3d=3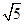 ,解得d=
,解得d=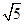 。易知(1)
。易知(1)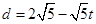 =
=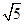 ,t=2(舍去)
,t=2(舍去)(2)
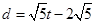 =
=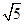 ,解得t=3
,解得t=3点评:本题难度较大。主要考查直角坐标系与相似三角形等综合运用。正确做出图像是解题关键。

练习册系列答案
相关题目
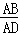 等于 .
等于 .
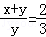 ;②
;②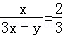 ;③
;③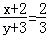 ;
;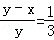 ;⑤
;⑤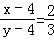 .
.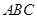 中,∠
中,∠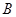 =30°,
=30°,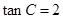 ,
,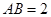 ,求△
,求△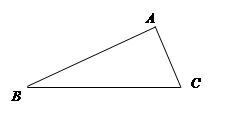
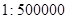 的地图上,A、B两点的距离为30厘米,那么A、B两地的实际距离是()
的地图上,A、B两点的距离为30厘米,那么A、B两地的实际距离是()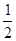 CD。
CD。