题目内容
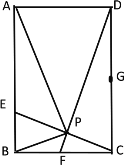
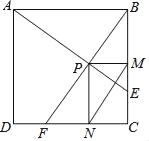
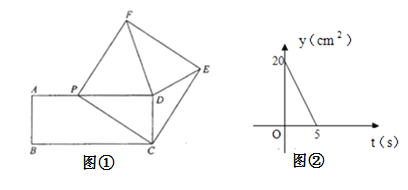
【题目】如图①,在矩形![]() 中,动点
中,动点![]() 从点
从点![]() 出发,以2cm/s的速度沿
出发,以2cm/s的速度沿![]() 向终点
向终点![]() 移动,设移动时间为t(s).连接
移动,设移动时间为t(s).连接![]() ,以
,以![]() 为一边作正方形
为一边作正方形![]() ,连接
,连接![]() 、
、![]() .设
.设![]() 的面积为
的面积为![]() (cm2).
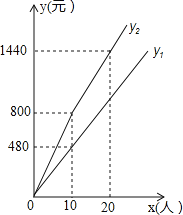
(cm2). ![]() 与t之间的函数关系如图②所示.
与t之间的函数关系如图②所示.
(1) ![]() cm,
cm,![]() cm;
cm;
(2) 点![]() 从点
从点![]() 到点
到点![]() 的移动过程中,点
的移动过程中,点![]() 的路径是_________________ cm.
的路径是_________________ cm.
(3)当![]() 为何值时,
为何值时,![]() 的面积最小?并求出这个最小值;
的面积最小?并求出这个最小值;
(4) 当![]() 为何值时,
为何值时,![]() 为等腰三角形?请直接写出结果。
为等腰三角形?请直接写出结果。
【答案】(1)4,10; (2)10; (3)当t=4时,最小值为6;(4)t=1,3,4 .
【解析】
(1)根据图②三角形PCD的面积,可得矩形的长和宽;
(2)由题意得:AP=t,PD=5-t,根据三角形面积公式可得y与t的关系式,由图②得:S△DEF+S△PDC=![]() S正方形EFPC,代入可得结论;
S正方形EFPC,代入可得结论;
(3)当△DEF为等腰三角形时,分三种情况进行讨论,根据全等三角形的性质计算PD和AP的长,可得t的值.
(1)由图②知:AD=5,
当t=0时,P与A重合,y=![]() ×AD×CD=5,
×AD×CD=5,
![]() ×5×CD=5,
×5×CD=5,
CD=2cm,
∵四边形ABCD是矩形,
∴AB=CD=2cm,
故答案为:2,5;
(2)由题意得:AP=t,PD=5-t,
∴y=![]() CDPD=
CDPD=![]() 2(5t)=5-t,
2(5t)=5-t,
∵四边形EFPC是正方形,
∴S△DEF+S△PDC=![]() S正方形EFPC,
S正方形EFPC,
∵PC2=PD2+CD2,
∴PC2=22+(5-t)2=t2-10t+29,
∴S△DEF=![]() (t2-10t+29)-(5-t)=
(t2-10t+29)-(5-t)=![]() t2-4t+
t2-4t+![]() =
=![]() (t-4)2+
(t-4)2+![]() ,
,
当t为4时,△DEF的面积最小,且最小值为![]() ;
;
(3)当△DEF为等腰三角形时,分三种情况:
①当FD=FE时,如下图所示,过F作FG⊥AD于G,
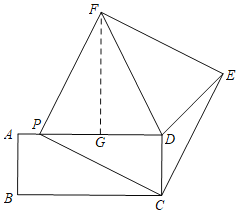
∵四边形EFPC是正方形,
∴PF=EF=PC,∠FPC=90°,
∴PF=FD,
∵FG⊥PD,
∴PG=DG=![]() PD,
PD,
∵∠FPG+∠CPD=∠CPD+∠DCP=90°,
∴∠FPG=∠DCP,
∵∠FGP=∠PDC=90°,
∴△FPG≌△PDC(AAS),
∴PG=DC=2,
∴PD=4,
∴AP=5-4=1,
即t=1;
②当DE=D时,如下图所示,E在AD的延长线上,此时正方形EFPC是正方形,PD=CD=2
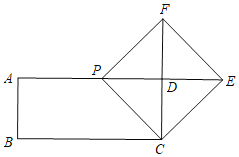
∴AP=t=5-2=3
③当DE=EF时,如下图所示,过E作EG⊥CD于G,
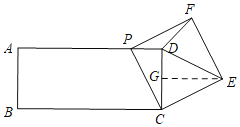
∵FE=DE=EC,
∴CG=DG=![]() CD=1,
CD=1,
同理得:△PDC≌△CGE(AAS),
∴PD=CG=1,
∴AP=t=5-1=4,
综上,当t=1s或3s或4s时,△DEF为等腰三角形.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案