题目内容
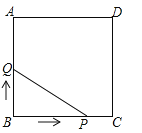
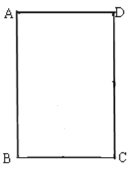
【题目】如图,矩形ABCD 中,AD=4cm,AB=6cm,动点 E从 B向A运动,速度为每秒2cm;同时,动点F从 C向B运动,速度为每秒3cm;任意一点到达终点后,两点都停止运动。连接CE、DF交于点P,连接BP,
(1)求证:△EBC ∽ △FCD
(2)BP最小值是多少?此时点F运动了多少秒?
(3)在该运动过程中, tan∠PAD的最大值是多少?

【答案】(1)详见解析;(2)BP最小值是2,此时点F运动了1秒;(3)最大值为![]()
【解析】
(1)根据点E、F的运动速度可得![]() ,易证△EBC ∽ △FCD;
,易证△EBC ∽ △FCD;
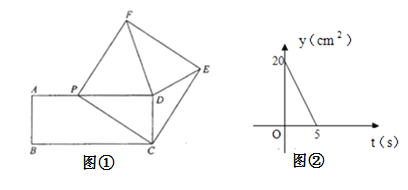
(2)由(1)可得∠DPC=90°,推出点P落在以CD为直径的圆弧上,当点B、P、G共线时,BP取最小值,此时可求出BP;作GH∥BC,利用相似三角形△BFP∽△GHP,可求出t.
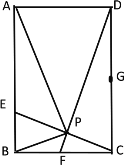
(3)在运动过程中,∠PAD的角度逐渐变大,所以当F运动到B点时,tan∠PAD最大,过点P作MN∥AB,由△BPC∽△CPD,△BNP∽△DMP和△BNP∽△BCD,利用对应边成比例可求出此时PM、BN的长度,易得tan∠PAD.
解:(1)设运动时间为t,则BE=2t,CF=3t,
∴![]() ,
,
又∵∠EBC=∠FCD=90°,
∴△EBC∽△FCD;
(2)∵△EBC∽△FCD,
∴∠ECB=∠FDC,
∵∠FDC+∠DFC=90°,
∴∠ECB+∠DFC=90°,
∴∠FPC=90°,即∠DPC=90°,
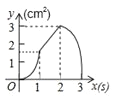
故点P落在以CD为直径的圆弧上,如图1,
令CD中点为G,运动时间为t,
∴当点B、P、G共线时,BP取最小值,
∴CG=![]() ,
,
∴BG=![]() ,
,
∴BP=BG-GP=5-3=2,
作GH∥BC,
则△BFP∽△GHP,GH=![]() ,BF=4-3t,
,BF=4-3t,
∴![]() ,即
,即 ,
,
解得:t=1;
(3)根据题意可知,在运动过程中,∠PAD的角度逐渐变大,
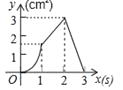
∴当F运动到B点时,tan∠PAD最大,
如图2,过点P作MN∥AB,
由∠BPC=90°易证△BPC∽△CPD,
∴![]() ,
,
设BP=2a,则PC=3a,PD=![]() ,
,
∵AD∥BC,
∴△BNP∽△DMP,
∴ ,
,
∴PM=![]() ,
,
由△BNP∽△BCD,可得 ,
,
∴BN=![]() ,
,
∴tan∠PAD= .
.