题目内容
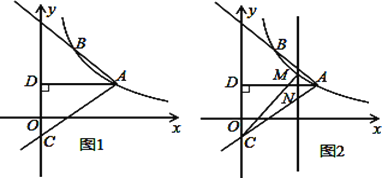
【题目】如图1,反比例函数![]() 的图象经过点A(
的图象经过点A(![]() ,1),射线AB与反比例函数图象交与另一点B(1,
,1),射线AB与反比例函数图象交与另一点B(1, ![]() ),射线AC与
),射线AC与![]() 轴交于点C,
轴交于点C, ![]() 轴,垂足为D.
轴,垂足为D.
(1)求![]() 和a的值;
和a的值;
(2)直线AC的解析式;
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线![]() 轴,与AC相交于N,连接CM,求
轴,与AC相交于N,连接CM,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)y=
;(2)y=![]() x﹣1;(3)
x﹣1;(3)![]()
【解析】试题分析:(1)把A点代入反比例函数解析式可求得k,把B点坐标代入反比例函数解析式可求得a的值;
(2)过B作BH⊥AD于H,由A、B坐标可得出△ABH为等腰直角三角形,由条件可求得∠DAC=30°,在△ACD中,由勾股定理可求得CD、AC,可求得C点坐标,利用待定系数法可求得直线AC的解析式;
(3)可设出M点坐标为(t, ![]() ),从而可表示出N点坐标,则可用t表示出MN的长,则可用t表示出△CMN的面积,利用二次函数的性质可求得其最大值.
),从而可表示出N点坐标,则可用t表示出MN的长,则可用t表示出△CMN的面积,利用二次函数的性质可求得其最大值.
试题解析:(1)把A(2![]() ,1)代入y=
,1)代入y=![]() ,可得k=2
,可得k=2![]() ×1=2
×1=2![]() ,
,
∴反比例函数解析式为y=![]() ,
,
把B(1,a)代入反比例函数解析式y=![]() ,可得a=2
,可得a=2![]() ;
;
(2)作BH⊥AD于H,如图1,

∵B点坐标为(1,2![]() ),
),
∴AH=2![]() -1,BH=2
-1,BH=2![]() -1,
-1,
∴△ABH为等腰直角三角形,
∴∠BAH=45°,
∵∠BAC=75°,
∴∠DAC=∠BAC-∠BAH=30°,
∵AD=2![]() ,设CD=x,则AC=2x,
,设CD=x,则AC=2x,
∴由勾股定理可得CD=2,AC=4,
∴C点坐标为(0,-1),
设直线AC解析式为y=kx+b,
把A(2![]() ,1),C(0,-1)代入可得
,1),C(0,-1)代入可得
 ,解得
,解得 ,
,
∴直线AC解析式为y=![]() x-1;
x-1;
(3)设M点坐标为(t, ![]() )(0<t<1),
)(0<t<1),
∵直线l⊥x轴,与AC相交于点N,
∴N点坐标为(t, ![]() t-1),
t-1),
∴MN=![]() -(
-(![]() t-1)=
t-1)=![]() -
-![]() t+1,
t+1,
∴S△CMN=![]() t(
t(![]() -
-![]() t+1)=-
t+1)=-![]() t2+
t2+![]() t+
t+![]() ,
,
∴当t=-![]() =
=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .
.




