题目内容
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=300,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是:(▲)


A、②④ B、①③
C、②③④ D、①②③④


A、②④ B、①③
C、②③④ D、①②③④
D
∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
(含①的只有B和D,它们的区别在于有没有④.它们都是含30°的直角三角形,并且斜边是相等的),
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),故④正确.
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,故②正确;
∴AG=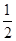 AF,
AF,
∴AG=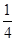 AB,
AB,
∵AD=AB,
则AD=AG,故③,
故选D.
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
(含①的只有B和D,它们的区别在于有没有④.它们都是含30°的直角三角形,并且斜边是相等的),
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),故④正确.
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,故②正确;
∴AG=
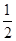 AF,
AF,∴AG=
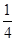 AB,
AB,∵AD=AB,
则AD=AG,故③,
故选D.

练习册系列答案
相关题目







