题目内容
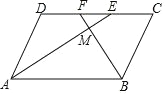
【题目】如图,BE平分∠ABC,∠ABC=2∠E,∠ADE+∠BCF=180°.
(1)请说明AB∥EF的理由;
(2)若AF平分∠BAD,判断AF与BE的位置关系,并说明理由.
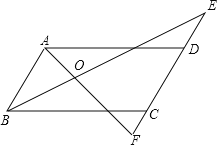
【答案】(1)见解析;(2)AF⊥BE,见解析.
【解析】
(1)结论:AB∥EF,只要证明∠E=∠ABE 即可;
(2)根据平行线的性质以及角平分线的定义即可证明.
(1)证明:∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC.
∠ABC.
又∵∠ABC=2∠E,
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠ABE.
∴AB∥EF;
(2)解:结论:AF⊥BE.
理由:∵∠ADE+∠ADF=180°,
∠ADE+∠BCF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
∴∠DAB+∠CBA=180°,
∵∠OAB=![]() DAB,∠OBA=
DAB,∠OBA=![]() ∠CBA,
∠CBA,
∴∠OAB+∠OBA=90°,
∴∠AOB=90°,
∴AF⊥BE.
故答案为:(1)见解析;(2)AF⊥BE,见解析.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目