题目内容
【题目】如图，二次函数y=（x﹣2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．
（1）求二次函数与一次函数的解析式；
（2）根据图象，写出满足kx+b≥（x﹣2）2+m的x的取值范围．
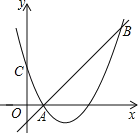
【答案】（1）二次函数解析式为y=（x﹣2）2﹣1；一次函数解析式为y=x﹣1．（2）1≤x≤4．
【解析】
（1）将点A（1，0）代入y=（x-2）2+m求出m的值，根据点的对称性，将y=3代入二次函数解析式求出B的横坐标，再根据待定系数法求出一次函数解析式．
（2）根据图象和A、B的交点坐标可直接求出kx+b≥（x-2）2+m的x的取值范围．
解：（1）将点A（1，0）代入y=（x﹣2）2+m得，（1﹣2）2+m=0，解得m=﹣1．
∴二次函数解析式为y=（x﹣2）2﹣1．
当x=0时，y=4﹣1=3，∴C点坐标为（0，3）．
∵二次函数y=（x﹣2）2﹣1的对称轴为x=2， C和B关于对称轴对称，
∴B点坐标为（4，3）．
将A（1，0）、B（4，3）代入y=kx+b得，
，解得
．
∴一次函数解析式为y=x﹣1．
（2）∵A、B坐标为（1，0），（4，3），
∴当kx+b≥（x﹣2）2+m时，直线y=x﹣1的图象在二次函数y=（x﹣2）2﹣1的图象上方或相交，此时1≤x≤4．
练习册系列答案
相关题目
