题目内容
已知函数y=-kx+4与y=
的图象有两个不同的交点，且A（-
，y1）、B（-1，y2）、C（
，y3）在函数y=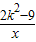
的图象上，则y1，y2，y3的大小关系是（ ）A．y1＜y2＜y3
B．y3＜y2＜y1
C．y3＜y1＜y2
D．y2＜y3＜y1
【答案】分析：由y=-kx+4与y=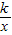
列出方程组，求出它们图象有两个不同的交点时k的范围，然后确定2k2-9的正负再比较y1，y2，y3的大小关系．
解答：解：把y=-kx+4代入y=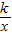
得，-kx+4=
，
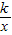化简得kx2-4x+k=0，
因为有两个不同的交点，
所以16-4k2＞0，2k2＜8，从而2k2-9＜0，
函数y=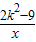
的图象在第二，四象限，
在每个象限内，y随x的增大而增大，
所以0＜y2＜y1，y3＜0，故y3＜y2＜y1．
故选B．
点评：本题本题考查了反比例函数图象的增减性等内容，范围比较广，难度大．
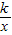列出方程组，求出它们图象有两个不同的交点时k的范围，然后确定2k2-9的正负再比较y1，y2，y3的大小关系．解答：解：把y=-kx+4代入y=
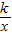得，-kx+4=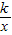，化简得kx2-4x+k=0，
因为有两个不同的交点，
所以16-4k2＞0，2k2＜8，从而2k2-9＜0，
函数y=
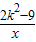的图象在第二，四象限，在每个象限内，y随x的增大而增大，
所以0＜y2＜y1，y3＜0，故y3＜y2＜y1．
故选B．
点评：本题本题考查了反比例函数图象的增减性等内容，范围比较广，难度大．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
已知函数y=
(k＞0)，当k取不同的数值时，可以得到许多不同的双曲线，这些双曲线必定（ ）
| k |
| x |
| A、交于同一个交点 |
| B、有无数个交点 |
| C、没有交点 |
| D、不能确定 |
已知函数y=
，当x=1时，y=-3，那么这个函数的解析式是（ ）
| k |
| x |
A、y=
| ||
B、y=
| ||
| C、y=3x | ||
| D、y=-3x |
已知函数y=kx+b的图象经过A（-2，-1）、B（1，3）两点，分别交x、y轴于点C、D．