题目内容
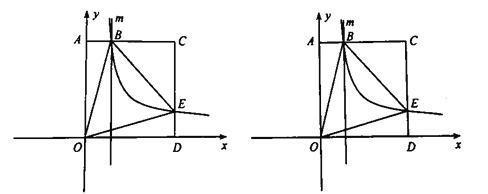
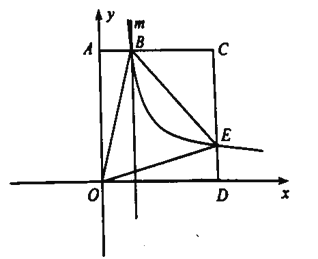
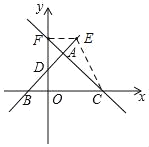
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点C与直线AD交于点A(1,2),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,请判断△ABC的形状;
(3)在直线AD上是否存在一点E,使得4S△BOD=S△ACE,若存在求出点E的坐标,若不存在说明理由.

【答案】(1)y=x+1;(2)△ABC是等腰直角三角形;(3)存在,点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.
【解析】
(1)利用待定系数法,即可得到直线AD的解析式;
(2)依据点的坐标求得AB=2![]() ,AC=2
,AC=2![]() ,BC=4,即可得到AB2+AC2=16=BC2,进而得出△ABC是等腰直角三角形;
,BC=4,即可得到AB2+AC2=16=BC2,进而得出△ABC是等腰直角三角形;
(3)依据4S△BOD=S△ACE,即可得到AE=![]() ,分两种情况进行讨论:①点E在直线AC的右侧,②点E在直线AC的左侧,分别依据AD=AE=
,分两种情况进行讨论:①点E在直线AC的右侧,②点E在直线AC的左侧,分别依据AD=AE=![]() ,即可得到点E的坐标.
,即可得到点E的坐标.
解:(1)直线AD的解析式为y=kx+b,
∵直线AD经过点A(1,2),点D(0,1),
∴![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1;
(2)∵y=x+1中,当y=0时,x=﹣1;y=﹣x+3中,当y=0时,x=3,
∴直线AD与x轴交于B(﹣1,0),直线AC与x轴交于C(3,0),
∵点A(1,2),
∴AB=2![]() ,AC=2
,AC=2![]() ,BC=4,
,BC=4,
∵AB2+AC2=16=BC2,
∴∠BAC=90°,
∴△ABC是等腰直角三角形;
(3)存在,
AC=2![]() ,S△BOD=
,S△BOD=![]() ×1×1=
×1×1=![]() ,
,
∵△ABC是等腰直角三角形,
∴∠CAE=90°,
∵S△ACE=![]() AE×AC,4S△BOD=S△ACE,
AE×AC,4S△BOD=S△ACE,
∴4×![]() =
=![]() ×AE×2
×AE×2![]() ,
,
解得AE=![]() ,
,
①如图,当点E在直线AC的右侧时,过E作EF⊥y轴于F,
∵AD=AE=![]() ,∠EDF=45°,
,∠EDF=45°,
∴EF=DF=2,OF=2+1=3,
∴E(2,3);
②当点E在直线AC的左侧时,
∵AD=AE=![]() ,
,
∴点E与点D重合,即E(0,1),
综上所述,当点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案