题目内容
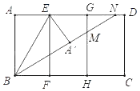
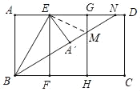
【题目】如图,矩形纸片ABCD,AB=8,AE=EG=GD=4,AB∥EF∥GH.将矩形纸片沿BE折叠,得到△BA′E(点A折叠到A′处),展开纸片;再沿BA′折叠,折痕与GH,AD分别交于点M,N,然后将纸片展开.
(1)连接EM,证明A′M=MG;
(2)设A′M=MG=x,求x值.
【答案】(1)见解析;(2)A′M=6﹣2![]() .
.
【解析】
(1)由翻折的性质得到A'E=EG,由矩形的性质好而其他条件得∠EGM=90°,从而得到Rt△EA'M≌Rt△EGM(HL),则A′M=MG;
(2)由已知条件,根据勾股定理得到BE的值,再由已知条件得到![]() ,设A′M=MG=x,从而得到x的值.
,设A′M=MG=x,从而得到x的值.
(1)连接EM,如图.
由折叠可知EA=EA',
∵AE=EG,∠EA'B=∠A=90°
∴A'E=EG,
∵四边形ABCD为矩形,AB∥EF∥GH,
∴∠EGM=90°
∴∠EGM=∠EA'M,
∴Rt△EA'M≌Rt△EGM(HL),
∴A′M=MG;
(2)∵AB=8,AE=4,
∴BE=![]() ,
,
∴EN=BE=![]() ,
,
∵AB∥EF∥GH,AE=EG=GD=4,AB=8,
∴![]() ,
,
设A′M=MG=x,
![]()
x=6﹣2![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?