题目内容
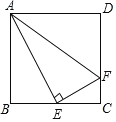
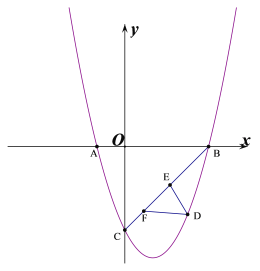
【题目】如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式.
(2)如图,直线BC下方的抛物线上有一点D,过点D作DE⊥BC于点E,作DF平行x轴交直线BC于点F,求△DEF周长的最大值.
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线对称轴的右侧,是否存在以点P,M,N,Q为顶点且以PM为边的正方形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)△DEF周长的最大值为
;(2)△DEF周长的最大值为![]() ;(3)点P的横坐标为2或
;(3)点P的横坐标为2或![]() .
.
【解析】
(1)把A,B两点代入求出解析式即可;
(2)由等腰直角三角形的性质可得![]() ,可得△DEF周长=DE+EF+DF=
,可得△DEF周长=DE+EF+DF=![]() ,设点D的坐标为
,设点D的坐标为![]() ,则点F的坐标为:
,则点F的坐标为:![]() ,求出最大值即可;
,求出最大值即可;
(3)分两种情况讨论,由正方形的性质和全等三角形的性质可求解.
解:(1)∵物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,
∴![]()
解得:![]() ,
,
∴解析式为:![]() ;
;
(2)∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴点C坐标为(0,-3),
∴直线BC解析式为:y=x-3,
∵点B(3,0),点C(0,-3),
∴OB=OC=3,
∴∠OBC=∠OCB=45°,
∵DF∥AB,
∴∠EFD=45°=∠OBC,
∵DE⊥BC,
∴∠EFD=∠EDF=45°,
∴DE=EF,
∴![]()
∴![]()
∴△DEF周长=DE+EF+DF=![]()
设点D的坐标为![]() ,则点F的坐标为:
,则点F的坐标为:![]() ,
,
∴DF=![]() ,
,
∴当![]() 时,DF有最大值为
时,DF有最大值为![]() ,
,
∴△DEF周长=![]() ;
;
(3)存在,
如图1,过点M作GH⊥OC,过点P作PH⊥GH,连接MN,PM,
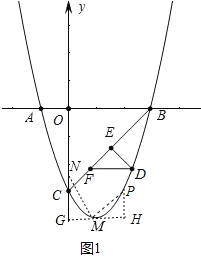
∵抛物线的解析式为![]() ,
,
∴点M(1,4),
∵以点P、M、N、Q为顶点且以PM为边的正方形,
∴PM=MN,∠PMN=90°,
∴∠PMH+∠NMG=90°,且∠PMH+∠MPH=90°,
∴∠NMG=∠MPH,且MN=PM,∠H=∠NGM=90°,
∴△MNG≌△PMH(AAS),
∴GM=PH=1,
∴点P的纵坐标为-3,
∴![]() ,
,
∴x=0(不合题意舍去),x=2,
∴点P的横坐标为2,
如图2,过点P作GH⊥AB,过点N作NG⊥GH,过点M作MH⊥GH,
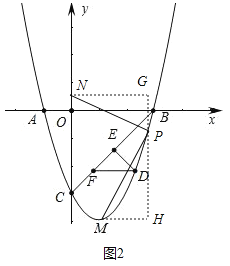
∴△NGP≌△PHM,
可得NG=PH,GP=MH,
设点P横坐标为m,(m>1)
∴NG=PH=m,
∴点P纵坐标为-4+m,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
综上所述:点P的横坐标为2或![]() .
.

【题目】某校七年级计划成立学生社团,要求每一位学生都选择一个社团而且只能选择一个社团.为了解学生对不同社团的选择意向,随机抽取了七年级部分学生进行“我最喜爱的社团”问卷调查,并将调查结果绘制成如下两个不完整的统计图表.
七年级部分学生“我最喜爱的社团”调查结果统计表
社团名称 | 人数 |
文学社团 | 4 |
创客社团 | 9 |
书法社团 |
|
绘画社团 | 6 |
体育社团 | 10 |
音乐社团 | 5 |
美食社团 |
|
数学社团 | 2 |
七年级部分学生“我最喜爱的社团”调查结果扇形统计图
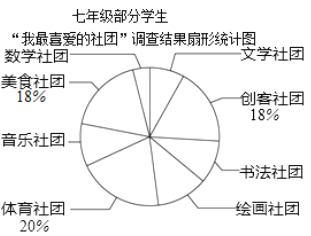
请解答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在扇形统计图中,“绘画社团”所对应的扇形圆心角为______度.
(3)该校七年级共有350名学生,每个社团人数不低于30人才可以开展.试通过计算估计该校七年级有哪些社团可以开展.
【题目】课外阅读是提高学生素养的重要途径.某中学为了了解全校学生课外阅读情况,随机抽查了200名学生,统计他们平均每天课外阅读时间(小时).根据每天课外阅读时间的长短分为A,B,C.D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
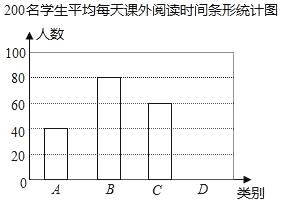
200名学生平均每天课外阅读时间统计表
类别 | 时间t(小时) | 人数 |
A | t<0.5 | 40 |
B | 0.5≤t<1 | 80 |
C | 1≤t<1.5 | 60 |
D | t≥1.5 | a |
(1)求表格中a的值,并在图中补全条形统计图:
(2)该校现有1800名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
(3)请你根据上述信息对该校提出相应的建议