题目内容
已知:有理数a、b、c满足abc<0,且a+b+c>0,当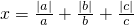 时,求代数式x19-95x+1028的值.
时,求代数式x19-95x+1028的值.
解:∵abc<0,a+b+c>0,
∴符合条件的只有一种情况:其中一个为负数,其余两个为正数,
分为以下三种情况:①当a<0时,b>0,c>0,
x=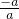 +
+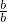 +
+ =-1+1+1=1,
=-1+1+1=1,
x19-95x+1028=1-95+1028=934;
②当b<0时,a>0,c>0,
x= +
+ +
+ =1-1+1=1,
=1-1+1=1,
x19-95x+1028=1-95+1028=934;
③当c<0时,a>0,b>0,
x= +
+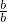 +
+ =1+1-1=1,
=1+1-1=1,
x19-95x+1028=1-95+1028=934;
即x19-95x+1028=934;
分析:根据已知得出其中一个为负数,其余两个为正数,分为三种情况:①当a<0时,b>0,c>0,②当b<0时,a>0,c>0,③当c<0时,a>0,b>0,求出x的值,代入求出即可.
点评:本题考查了求代数式的值,解此题的关键是求出x的值,题目比较好,有一定的难度,注意:当a<0时,|a|=-a.
∴符合条件的只有一种情况:其中一个为负数,其余两个为正数,
分为以下三种情况:①当a<0时,b>0,c>0,
x=
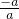 +
+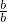 +
+ =-1+1+1=1,
=-1+1+1=1,x19-95x+1028=1-95+1028=934;
②当b<0时,a>0,c>0,
x=
 +
+ +
+ =1-1+1=1,
=1-1+1=1,x19-95x+1028=1-95+1028=934;
③当c<0时,a>0,b>0,
x=
 +
+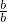 +
+ =1+1-1=1,
=1+1-1=1,x19-95x+1028=1-95+1028=934;
即x19-95x+1028=934;
分析:根据已知得出其中一个为负数,其余两个为正数,分为三种情况:①当a<0时,b>0,c>0,②当b<0时,a>0,c>0,③当c<0时,a>0,b>0,求出x的值,代入求出即可.
点评:本题考查了求代数式的值,解此题的关键是求出x的值,题目比较好,有一定的难度,注意:当a<0时,|a|=-a.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

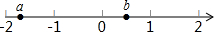 已知,有理数a,b在数轴上的位置如图所示:
已知,有理数a,b在数轴上的位置如图所示: