题目内容
（2012•黑河）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2-7x+12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点0运动；同时，动点Q从
点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
（1）求A、B两点的坐标．
（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．
（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．
点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．（1）求A、B两点的坐标．
（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．
（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．
分析：（1）解一元二次方程，求出OA、OB的长度，从而得到A、B点的坐标；
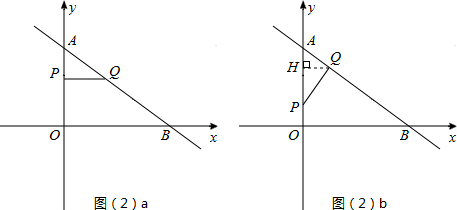
（2）△APQ与△AOB相似时，存在两种情况，需要分类讨论，不要遗漏，如图（2）所示；
（3）本问关键是找齐平行四边形的各种位置与性质，如图（3）所示．在求M1，M2坐标时，注意到M1，M2与Q点坐标的对应关系，则容易求解；在求M3坐标时，可以利用全等三角形，得到线段之间关系．
（2）△APQ与△AOB相似时，存在两种情况，需要分类讨论，不要遗漏，如图（2）所示；
（3）本问关键是找齐平行四边形的各种位置与性质，如图（3）所示．在求M1，M2坐标时，注意到M1，M2与Q点坐标的对应关系，则容易求解；在求M3坐标时，可以利用全等三角形，得到线段之间关系．
解答：解：（1）解方程x2-7x+12=0，得x1=3，x2=4，
∵OA＜OB，∴OA=3，OB=4．
∴A（0，3），B（4，0）．
（2）在Rt△AOB中，OA=3，OB=4，∴AB=5，∴AP=t，QB=2t，AQ=5-2t．
△APQ与△AOB相似，可能有两种情况：
（I）△APQ∽△AOB，如图（2）a所示．
则有
=
，即
=
，解得t=
．
此时OP=OA-AP=
，PQ=AP•tanA=
，∴Q（
，
）；
（II）△APQ∽△ABO，如图（2）b所示．
则有
=
，即
=
，解得t=
．
此时AQ=
，AH=AQ•cosA=
，HQ=AQ•sinA=
，OH=OA-AH=
，∴Q（
，
）．
综上所述，当t=
秒或t=
秒时，△APQ与△AOB相似，所对应的Q点坐标分别为（
，
）或（
，
）．
（3）结论：存在．如图（3）所示．
∵t=2，∴AP=2，AQ=1，OP=1．
过Q点作QE⊥y轴于点E，则QE=AQ•sin∠QAP=
，AE=AQ•cos∠QAP=
，
∴OE=OA-AE=
，∴Q（
，
）．
∵?APQM1，∴QM1⊥x轴，且QM1=AP=2，∴M1（
，
）；
∵?APQM2，∴QM2⊥x轴，且QM2=AP=2，∴M2（
，
）；
如图（3），过M3点作M3F⊥y轴于点F，
∵?AQPM3，∴M3P=AQ，∠QAE=∠M3PF，∴∠PM3F=∠AQE；
在△M3PF与△QAE中，∵∠QAE=∠M3PF，M3P=AQ，∠PM3F=∠AQE，
∴△M3PF≌△QAE，
∴M3F=QE=
，PF=AE=
，∴OF=OP+PF=
，∴M3（-
，
）．
∴当t=2时，在坐标平面内，存在点M，使以A、P、Q、M为顶点的四边形是平行四边形．
点M的坐标为：M1（
，
），M2（
，
），M3（-
，
）．
∵OA＜OB，∴OA=3，OB=4．
∴A（0，3），B（4，0）．
（2）在Rt△AOB中，OA=3，OB=4，∴AB=5，∴AP=t，QB=2t，AQ=5-2t．
△APQ与△AOB相似，可能有两种情况：
（I）△APQ∽△AOB，如图（2）a所示．
则有
| AP |
| AO |
| AQ |
| AB |
| t |
| 3 |
| 5-2t |
| 5 |
| 15 |
| 11 |
此时OP=OA-AP=
| 18 |
| 11 |
| 20 |
| 11 |
| 20 |
| 11 |
| 18 |
| 11 |
（II）△APQ∽△ABO，如图（2）b所示．
则有
| AP |
| AB |
| AQ |
| AO |
| t |
| 5 |
| 5-2t |
| 3 |
| 25 |
| 13 |
此时AQ=
| 15 |
| 13 |
| 9 |
| 13 |
| 12 |
| 13 |
| 30 |
| 13 |
| 12 |
| 13 |
| 30 |
| 13 |
综上所述，当t=
| 15 |
| 11 |
| 25 |
| 13 |
| 20 |
| 11 |
| 18 |
| 11 |
| 12 |
| 13 |
| 30 |
| 13 |
（3）结论：存在．如图（3）所示．
∵t=2，∴AP=2，AQ=1，OP=1．
过Q点作QE⊥y轴于点E，则QE=AQ•sin∠QAP=
| 4 |
| 5 |
| 3 |
| 5 |
∴OE=OA-AE=
| 12 |
| 5 |
| 4 |
| 5 |
| 12 |
| 5 |
∵?APQM1，∴QM1⊥x轴，且QM1=AP=2，∴M1（
| 4 |
| 5 |
| 2 |
| 5 |
∵?APQM2，∴QM2⊥x轴，且QM2=AP=2，∴M2（
| 4 |
| 5 |
| 22 |
| 5 |
如图（3），过M3点作M3F⊥y轴于点F，
∵?AQPM3，∴M3P=AQ，∠QAE=∠M3PF，∴∠PM3F=∠AQE；
在△M3PF与△QAE中，∵∠QAE=∠M3PF，M3P=AQ，∠PM3F=∠AQE，
∴△M3PF≌△QAE，
∴M3F=QE=
| 4 |
| 5 |
| 3 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
∴当t=2时，在坐标平面内，存在点M，使以A、P、Q、M为顶点的四边形是平行四边形．
点M的坐标为：M1（
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 22 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
点评：本题是动点型压轴题，综合考查了相似三角形的判定与性质、全等三角形的判定与性质、解一元二次方程、平行四边形等知识点．本题难点在于分类讨论思想的应用，第（2）（3）问中，均涉及到多种情况，需要逐一分析不能遗漏；另外注意解答中求动点时刻t和点的坐标的过程中，全等三角形、相似三角形、三角函数等知识发挥了重要作用，这是解答压轴题的常见技巧，需要熟练掌握．
练习册系列答案
相关题目
（2012•黑河）如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2012的坐标为
（2012•黑河）如图所示，沿DE折叠长方形ABCD的一边，使点C落在AB边上的点F处，若AD=8，且△AFD的面积为60，则△DEC的面积为
（2012•黑河）如图，已知AC=BD，要使△ABC≌△DCB，则只需添加一个适当的条件是
（2012•黑河）如图，抛物线y=-