题目内容
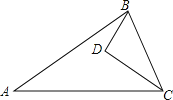
【题目】在![]() 中,点E,点F分别是边AC,AB上的点,且
中,点E,点F分别是边AC,AB上的点,且![]() ,连结BE,CF交于点D,
,连结BE,CF交于点D,![]() .
.

(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)∠BEC=50°
【解析】
(1)根据条件直接利用AAS判定△ABE≌△ACF,得到AB=AC,推出∠ABC=∠ACB,结合∠ABE=∠ACF可推出∠DBC=∠DCB,即可判定△BCD为等腰三角形;
(2)先由∠A=40°和AB=AC求出∠ACB的度数,然后根据∠DBC=∠DCB得到DB=DC,再由BC=BD可推出△BCD为等边三角形,利用∠BEC=180°-∠BCE-∠EBC,即可求出∠BEC的度数.
证明:(1)在△ABE和△ACF中,

∴△ABE≌△ACF(AAS)
∴AB=AC
∴∠ABC=∠ACB
又∵∠ABE=∠ACF
∴∠ABC-∠ABE=∠ACB-∠ACF
即∠DBC=∠DCB
∴DB=DC
∴△BCD为等腰三角形.
(2)∵∠A=40°,AB=AC,
∴∠ACB=![]()
∵DB=DC,BC=BD
∴DB=DC=BC
∴△BCD为等边三角形
∴∠EBC=60°
∴∠BEC=180°-∠BCE-∠EBC=180°-70°-60°=50°

练习册系列答案
相关题目