题目内容
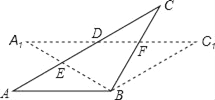
【题目】在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正确的有
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
【答案】C
【解析】
①两个不同的三角形中有两个角相等,那么第三个角也相等;
②根据ASA进而得出△A1BF≌△CBE,即可得出A1E=CF;
③∠CDF=α,而∠C与顺时针旋转的度数不一定相等,所以DF与FC不一定相等;
④AE不一定等于CD,则AD不一定等于CE,
⑤用角角边可证明△A1BF≌△CBE后可得A1F=CE.
∵△ABC绕点B顺时针旋转α度,得到△A1BC1,
∴∠CBC1=α,∠C=∠C1,
∵∠BFC1=∠DFC,
∴∠CDF=∠CBC1=α,故①正确,
∵AB=BC,
∴∠A=∠C,
∴∠C=∠A1
在△A1BF和△CBE中,
∠C=∠A1,A1B=BC,∠A1BF=∠CBE,
∴△A1BF≌△CBE,
∴BE=BF,A1F=CE,故⑤正确,
∵A1B=BC,
∴A1B-BE=BC-BF,即A1E=CF,故②正确,
∵∠CDF=α,α是可变化的角,∠C是固定角,
∴∠CDF不一定等于∠C,
∴DF不一定等于CF,故③错误,
∵AE不一定等于CD,
∴AD不一定等于CE,故④错误.
综上所述:①②⑤正确,
故选C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 计算“
计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
![]() 小颖说:“根据实验,一次实验中出现
小颖说:“根据实验,一次实验中出现![]() 点朝上的概率最大”;小红说:“如果投掷
点朝上的概率最大”;小红说:“如果投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
![]() 小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为
小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为![]() 的倍数的概率.
的倍数的概率.