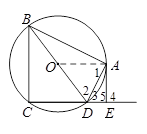题目内容
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在
AC的延长线上,且∠CBF=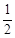 ∠CAB.
∠CAB.
(Ⅰ)求证:直线BF是⊙O的切线;
(Ⅱ)若AB=5,sin∠CBF= ,求BC和BF的长.
,求BC和BF的长.
AC的延长线上,且∠CBF=
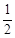 ∠CAB.
∠CAB.
(Ⅰ)求证:直线BF是⊙O的切线;
(Ⅱ)若AB=5,sin∠CBF=
 ,求BC和BF的长.
,求BC和BF的长.(Ⅰ)证明:连接AE.
∵AB为⊙O的直径,∴∠AEB=90°.
∴∠EAB+∠ABE=90°.
∵ AB="AC" , ∴∠EAB=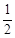 ∠CAB .
∠CAB .
∵∠CBF=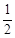 ∠CAB , ∴∠EAB =∠CBF,
∠CAB , ∴∠EAB =∠CBF,
∴ ∠CBF+∠ABE=90°,即∠ABF==90°.
∵AB是⊙O的直径,∴ 直线BF是⊙O的切线.
(Ⅱ)解:过点C作CG⊥AB于点G .
∵sin∠CBF= ,∠EAB =∠CBF, ∴sin∠EAB=
,∠EAB =∠CBF, ∴sin∠EAB= ,
,
∵∠AEB=90°,AB=5,∴BE= AB·sin∠EAB=
∵AB=AC,∠AEB=90°,∴BC="2" BE=2 .
.
在Rt△ABE中,AE= =2
=2 .
.
∴ sin∠ABE=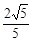 ,cos∠ABE=
,cos∠ABE= .
.
在Rt△CBG中,可求得GC=4,GB="2" ,∴ AG="3" .
∵CG∥BF,∴△AGC∽△ABF,
∴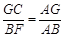 ,∴BF=
,∴BF=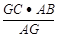 =
=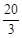 .
.
∵AB为⊙O的直径,∴∠AEB=90°.
∴∠EAB+∠ABE=90°.
∵ AB="AC" , ∴∠EAB=
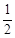 ∠CAB .
∠CAB . ∵∠CBF=
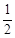 ∠CAB , ∴∠EAB =∠CBF,
∠CAB , ∴∠EAB =∠CBF, ∴ ∠CBF+∠ABE=90°,即∠ABF==90°.
∵AB是⊙O的直径,∴ 直线BF是⊙O的切线.
(Ⅱ)解:过点C作CG⊥AB于点G .
∵sin∠CBF=
 ,∠EAB =∠CBF, ∴sin∠EAB=
,∠EAB =∠CBF, ∴sin∠EAB= ,
,∵∠AEB=90°,AB=5,∴BE= AB·sin∠EAB=

∵AB=AC,∠AEB=90°,∴BC="2" BE=2
 .
. 在Rt△ABE中,AE=
 =2
=2 .
.∴ sin∠ABE=
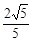 ,cos∠ABE=
,cos∠ABE= .
.在Rt△CBG中,可求得GC=4,GB="2" ,∴ AG="3" .
∵CG∥BF,∴△AGC∽△ABF,
∴
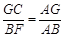 ,∴BF=
,∴BF=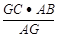 =
=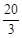 .
. (I)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(II)利用已知条件证得∴△AGC∽△BFA,利用比例式求得线段的长即可.
(II)利用已知条件证得∴△AGC∽△BFA,利用比例式求得线段的长即可.

练习册系列答案
相关题目
 ×100%
×100%
 =KD·GE,试判断AC与EF的位置关系,并说明理由;
=KD·GE,试判断AC与EF的位置关系,并说明理由;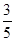 ,AK=
,AK=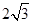 ,求FG的长.
,求FG的长.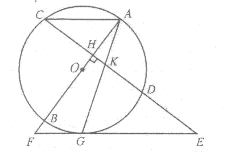
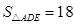 ,求四边形BCED的面积.
,求四边形BCED的面积.

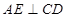 于点E,DA平分
于点E,DA平分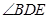 .
.