题目内容
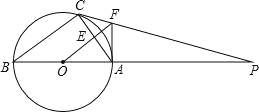
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,先证出∠3=∠2,由SAS证明△OAF≌△OCF,得对应角相等∠OAF=∠OCF,再根据切线的性质得出∠OCF=90°,证出∠OAF=90°,即可得出结论;
(2)先由勾股定理求出OF,再由三角形的面积求出AE,根据垂径定理得出AC=2AE.
试题解析:(1)连接OC,如图所示:
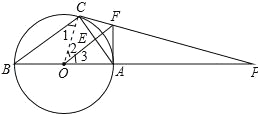
∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
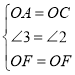 ,
,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)∵⊙O的半径为4,AF=3,∠OAF=90°,
∴OF=![]() =5
=5
∵FA⊥OA,OF⊥AC,
∴AC=2AE,△OAF的面积=![]() AFOA=
AFOA=![]() OFAE,
OFAE,
∴3×4=5×AE,
解得:AE=![]() ,
,
∴AC=2AE=![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目